ODKAZ NA tento dokument .DOC ZDE
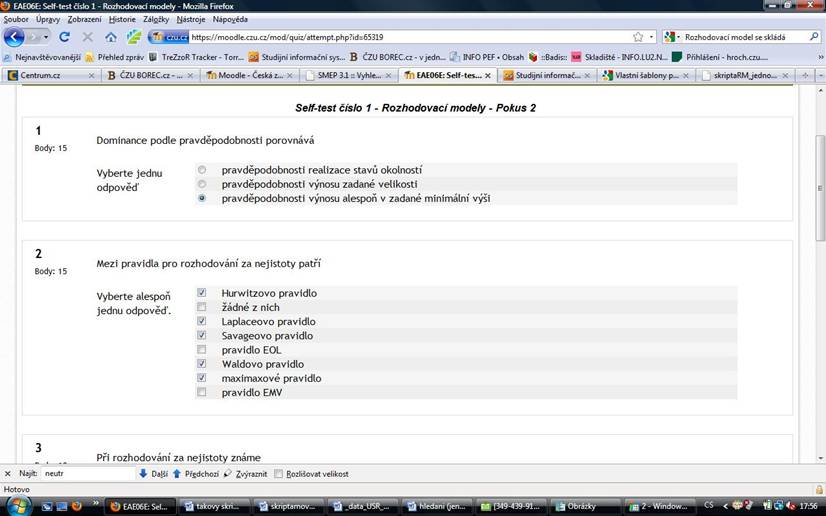
ODKAZ NA cviceni2
ODKAZ NA cviceni3
ODKAZ NA cviceni3_2
ODKAZ NA cviceni5
ODKAZ NA cviceni6
ODKAZ NA cviceni6_2
ODKAZ NA zapocet1
ODKAZ NA zapocet2
ODKAZ NA zapocet3
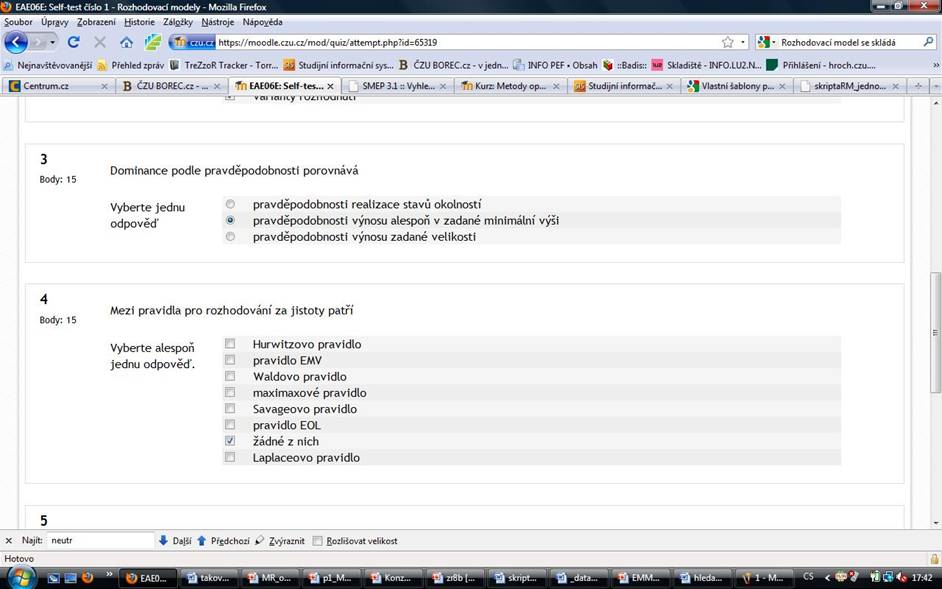
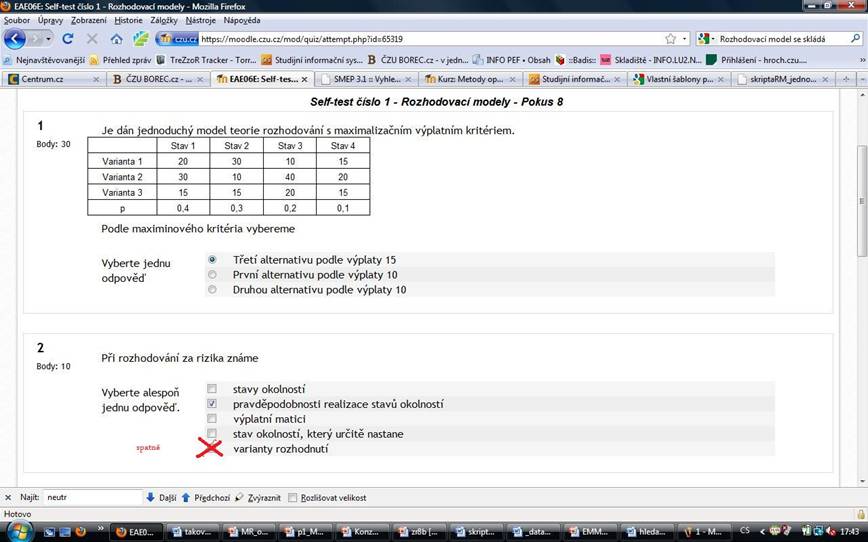
2
Body: 20
Tah je
Vyberte jednu odpověď
cíl hráče
výplata hráče
jeden krok z chování hráče ve hře toto jsem dal
chování hráče ve hře
Question 5
Body: 20
Které z následujících tvrzení platí pro řešení hry dvou inteligentních hráčů s nulovým součtem?
Pokud existuje řešení hry v oboru čistých strategií, dolní cena hry se rovná horní ceně hry. ... spra T
Pokud jeden z hráčů zvolí pro řešení konfliktní situace jinou než svoji optimální čistou strategii, vždy dosáhne horšího výsledku, než by mohl. ... spra T
Pokud existuje sedlový bod hry, hra nemá řešení v oboru čistých strategií. ... spra F
Pokud jsou ve výplatní matici pouze kladné hodnoty, hra je nespravedlivá. ... spra T
Pokud existuje sedlový bod hry, je reprezentován jedním nebo více poli ve výplatní matici. ... spra T
1
Body: 20
V nekooperativní hře nemůže být
Vyberte jednu odpověď
skupina inteligentních hráčů
skupina nespolupracujících hráčů
skupina neinteligentních hráčů
skupina spolupracujících hráčů (to je spravne)
4
Body: 20
V rozhodovacích situacích je hra definována jako
Vyberte jednu odpověď
oblíbená dětská činnost
ekonomický boj firem
hazardní hra
- konfliktní situace hráčů, kteří chtějí vyhrát
3
Body: 20
Rozdíl mezi hrou a partií lze vysvetlit takto:
Vyberte jednu odpověď
Jedno kolo partie je hra
Hra se skládá z partií
Hra a partie je totéž
- Opakování hry je partie (toto je spravne)
2
Body: 20
Které z následujících tvrzení platí pro řešení hry dvou inteligentních hráčů s nulovým součtem?
Pokud existuje řešení hry v oboru čistých strategií, dolní cena hry se rovná horní ceně hry. ... spra T
Pokud jeden z hráčů zvolí pro řešení konfliktní situace jinou než svoji optimální čistou strategii, vždy dosáhne horšího výsledku, než by mohl. ... spra T
Pokud existuje sedlový bod hry, hra nemá řešení v oboru čistých strategií. ... spra F
Pokud jsou ve výplatní matici pouze kladné hodnoty, hra je nespravedlivá. ... spra T
Pokud existuje sedlový bod hry, je reprezentován jedním nebo více poli ve výplatní matici. ... spra T
2
Body: 20
Které z následujících tvrzení platí pro řešení hry dvou inteligentních hráčů s nulovým součtem?
Pokud jsou ve výplatní matici pouze záporné hodnoty, hra je nespravedlivá. ... T
Pokud existuje sedlový bod hry, vždy je možné ve výplatní matici nalézt pouze jeden.
Pokud existuje řešení hry v oboru čistých strategií, dolní cena hry je menší než horní cena hry. ... F
Pokud jeden z hráčů zvolí pro řešení konfliktní situace jinou než svoji optimální čistou strategii, může dosáhnout lepšího výsledku než je horní cena hry. ... F
Pokud existuje sedlový bod hry, hra má řešení v oboru čistých strategií. ... T
mam z toho 16 b. a dal jsem
T
-
F
F
T
Body: 20
Strategie je
Vyberte jednu odpověď
- chování hráče ve hře
jeden krok z chování hráče ve hře
výplata hráče
cíl hráče
3
Body: 20
Rozhodněte o pravdivosti tvrzení:
Model hry v rozvinutém tvaru je reprezentován výplatní maticí. ... spra F
Každá maticová hra je řešitelná, ale někdy nelze určit optimální strategie hráčů i cenu hry. ... spra F
Strom hry je graf, který se skládá z uzlů a hran. ... spra T
Listy stromu hry představují výplaty hry pro dané kombinace strategií hráčů. ... spra T
Každá maticová hra je řešitelná v čistých strategiích. ... spra F
3
Body: 20
Tah je
Vyberte jednu odpověď
chování hráče ve hře
cíl hráče
výplata hráče
- jeden krok z chování hráče ve hře
5
Body: 20
Které z následujících tvrzení platí pro řešení hry dvou inteligentních hráčů s nulovým součtem?
Pokud jsou ve výplatní matici pouze kladné hodnoty, hra je nespravedlivá.
Pokud existuje řešení hry v oboru čistých strategií, dolní cena hry je menší než horní cena hry.
I když existuje sedlový bod hry, nemusí být reprezentován žádným polem ve výplatní matici.
Pokud jsou ve výplatní matici pouze kladné nebo záporné hodnoty, i přesto může být cena hry nulová.
Pokud existuje sedlový bod hry, hra má řešení v oboru čistých strategií.
mam z toho 16 b. a dal jsem
T
F
F (not sure)
F (not sure), spra je to T
T
Body: 20
Rozhodněte o pravdivosti tvrzení:
Model hry v normálním tvaru je reprezentován stromem hry.
Každá maticová hra je řešitelná, lze vždy najít optimální strategie hráčů a cenu hry.
Listy stromu hry představují výplaty hry pro dané kombinace strategií hráčů.
Model hry v rozvinutém tvaru je reprezentován výplatní maticí.
V jednotlivých hranách stromu hry volí hráči své tahy.
Uzly stromu hry zobrazují jednotlivé tahy ve hře.
Mam z toho 10 b. a dal jsem
F
F
F
F
F
T
-----
Question 2
Body: 20
Jestliže ve hře vždy jeden hráč vyhraje a druhý prohraje, pak
Vyberte alespoň jednu odpověď.
při bodování 1, 2 jde o hru s nenulovým součtem (tohle jsem zaskrt)
při bodování 1, -1 jde o hru s nekonstantním součtem
při bodování 1, 2 jde o hru s nekonstantním součtem
při bodování 1, -1 jde o hru s nenulovým součtem
tak je to spra
Question 3
Body: 20
Hráč má k dispozici 4 strategie. Řešením hry mohl dospět k následujícím doporučením. Přiřaďte jim správné označení.
„Hraj vždy strategii 4.“ cista strateg
„Hraj vždy strategii 3 nebo strategii 1.“ cista strateg
„Střídej strategie podle vektoru optimální strategie (0,8; 0; 0; 0,2)“ smisena strateg
„Střídej strategie podle vektoru optimální strategie (1; 0; 0; 0)“ smisena strateg
Tak z toho jsem mel 10 b.
-------
1
Body: 20
Hra s nulovým součtem je hra, ve které
Vyberte alespoň jednu odpověď.
součet výher hráčů je proměnlivý ... to asi ne
oba mohou vyhrát i prohrát (ztratit i získat)
oba hráči získají stejnou výhru
jeden hráč získá to, co druhý ztratí .... (tohle jsem zaskrt)
Question 3
Body: 20
Hráč má k dispozici 4 strategie. Řešením hry mohl dospět k následujícím doporučením. Přiřaďte jim správné označení.
„Hraj vždy strategii 3.“ dal jsem cista
„Střídej strategie podle vektoru optimální strategie (0; 0; 0; 1)“ dal jsem smisena
„Většinou hraj strategii 2, občas zkus některou z ostatních“ dal jsem smisena
„Střídej strategie podle vektoru optimální strategie (0,1; 0,1; 0,1; 0,7)“ dal jsem smisena
Tak z toho jsem mel 35 b.
----
Question 2
Body: 20
Hráč má k dispozici 4 strategie. Řešením hry mohl dospět k následujícím doporučením. Přiřaďte jim správné označení.
„Hraj vždy strategii 1.“ dal jsem cista
„Většinou hraj strategii 3, občas strategii 4, výjimečně strategii 1“ dal jsem smisena
„Střídej strategie podle vektoru optimální strategie (0; 0; 1; 0)“ dal jsem smisena
„Střídej strategie podle vektoru optimální strategie (0,2; 0,3; 0,1; 0,4)“ dal jsem smisena
Question 3
Body: 20
Které z následujících tvrzení platí pro řešení hry dvou inteligentních hráčů s nulovým součtem?
Pokud jsou ve výplatní matici pouze kladné hodnoty, hra je nespravedlivá. dal jsem T
Pokud existuje řešení hry v oboru čistých strategií, dolní cena hry je menší než horní cena hry. dal F
I když existuje sedlový bod hry, nemusí být reprezentován žádným polem ve výplatní matici. dal F
Pokud jsou ve výplatní matici pouze kladné nebo záporné hodnoty, i přesto může být cena hry nulová. dal T
Pokud existuje sedlový bod hry, hra má řešení v oboru čistých strategií. dal T
Question 5
Body: 20
Hra s konstantním součtem je hra, ve které
Vyberte alespoň jednu odpověď.
oba hráči získají stejnou výhru
oba mohou vyhrát (získat)
součet výher je konstantní dal jsem tohle
jeden hráč získá to, co druhý ztratí dal jsem tohle
Tak z toho mam 55 b.
---
Hráč má k dispozici 4 strategie. Řešením hry mohl dospět k následujícím doporučením. Přiřaďte jim správné označení.
„Hraj vždy strategii 3.“ dal jsem cista
„Střídej strategie podle vektoru optimální strategie (0; 0; 0; 1)“ dal jsem smisena
„Většinou hraj strategii 2, občas zkus některou z ostatních“ dal jsem smisena
„Střídej strategie podle vektoru optimální strategie (0,1; 0,1; 0,1; 0,7)“ dal jsem smisena
A mam z toho 15 b.
----
Question 2
Body: 20
Hráč má k dispozici 4 strategie. Řešením hry mohl dospět k následujícím doporučením. Přiřaďte jim správné označení.
„Hraj vždy strategii 4.“
„Hraj vždy strategii 3 nebo strategii 1.“
„Střídej strategie podle vektoru optimální strategie (0,8; 0; 0; 0,2)“
„Střídej strategie podle vektoru optimální strategie (1; 0; 0; 0)“
tady asi 5 b. ztrata
Question 3
Body: 20
V rozhodovacích situacích je hra definována jako
Vyberte jednu odpověď
hazardní hra
ekonomický boj firem
oblíbená dětská činnost
konfliktní situace hráčů, kteří chtějí vyhrát
snad ok
Question 4
Body: 20
Rozhodněte o pravdivosti tvrzení:
Model hry v rozvinutém tvaru je reprezentován výplatní maticí.
Každá maticová hra je řešitelná, ale někdy nelze určit optimální strategie hráčů i cenu hry.
Strom hry je graf, který se skládá z uzlů a hran.
Listy stromu hry představují výplaty hry pro dané kombinace strategií hráčů.
Každá maticová hra je řešitelná v čistých strategiích.
snad ok
Question 5
Body: 20
Jestliže ve hře vždy jeden hráč vyhraje a druhý prohraje nebo hra skončí remízou, pak
Vyberte alespoň jednu odpověď.
při bodování 1, -1, 0 jde o hru s konstantním součtem dal
při bodování 1, -1, 0 jde o hru s nulovým součtem dal
při bodování 1, 3, 2 jde o hru s konstantním součtem nedal
při bodování 1, 3, 2 jde o hru s nulovým součtem nedal
tu jsem ztratil 5 b.
Tak z toho mam 63 b.
----
1
Body: 20
Strategie je
Vyberte jednu odpověď
jeden krok z chování hráče ve hře
cíl hráče
- chování hráče ve hře dal
výplata hráče
Question 2
Body: 20
Rozhodněte o pravdivosti tvrzení:
Hrany stromu hry tvoří přípustné varianty tahu v dané partii hry. T
Model hry v normálním tvaru je reprezentován stromem hry. F
Listy stromu hry představují výplaty hry pro dané kombinace strategií hráčů. T
Model hry v rozvinutém tvaru je reprezentován výplatní maticí. F
Existuje maticová hra dvou inteligentních hráčů, pro kterou není možné najít optimální strategie hráčů. F
Uzly stromu hry tvoří rozhodovací problémy hráčů v jednotlivých tazích hry.
Question 4
Body: 20
Jestliže ve hře vždy jeden hráč vyhraje a druhý prohraje nebo hra skončí remízou, pak
Vyberte alespoň jednu odpověď.
při bodování 1, -1, 0 jde o hru s nulovým součtem dal
při bodování 1, -1, 0 jde o hru s konstantním součtem dal
při bodování 1, 3, 2 jde o hru s konstantním součtem dal
při bodování 1, 3, 2 jde o hru s nulovým součtem nedal
z tohohle jsem mel zrejme 15
Question 5
Body: 20
Hráč má k dispozici 4 strategie. Řešením hry mohl dospět k následujícím doporučením. Přiřaďte jim správné označení.
„Hraj vždy strategii 1.“ dal cista
„Většinou hraj strategii 3, občas strategii 4, výjimečně strategii 1“ dal cista
„Střídej strategie podle vektoru optimální strategie (0; 0; 1; 0)“ dal smisena
„Střídej strategie podle vektoru optimální strategie (0,2; 0,3; 0,1; 0,4)“ dal smisena
z tohohle jsem mel zrejme 15
Z toho mam 70 b.
---
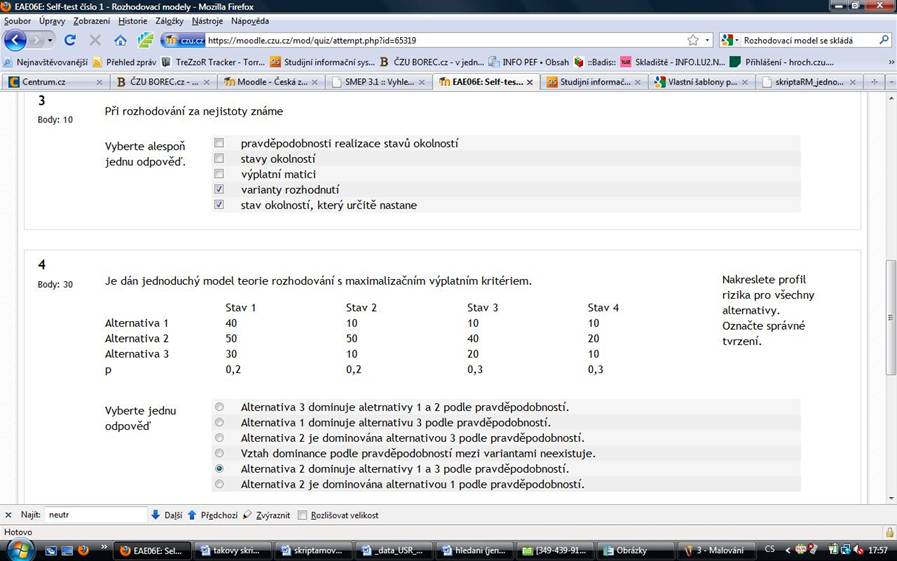
5
Body: 20
Určete dolní a horní cenu hry pro následující hru a rozhodněte o typu výsledku:
-10 10 -9 3
-1 10 2 8
0 -5 8 10
Dolní cena hry = dal -1
Horní cena hry = dal 10
Hra má řešení v oboru strategií. ... dal smisenych
za tohle mam 13 b.
---
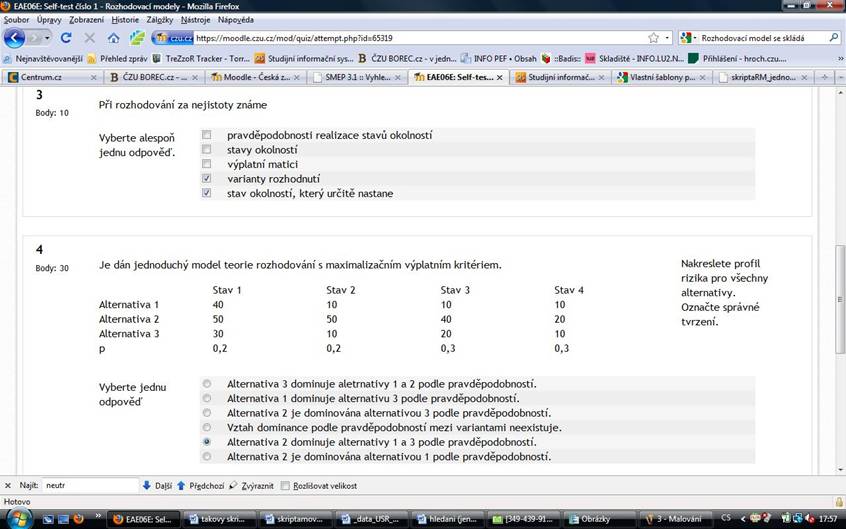
3
Body: 20
Určete dolní a horní cenu hry pro následující hru a rozhodněte o typu výsledku:
5 2 -1 3
7 3 2 5
-1 -5 1 10
Dolní cena hry = 2
Horní cena hry = 2
Hra má řešení v oboru strategií. cistych
A za tohle mam 20 b.
---
1
Body: 20
Rozdíl mezi hrou a partií lze vysvetlit takto:
Vyberte jednu odpověď
Jedno kolo partie je hra
Hra a partie je totéž
Opakování hry je partie dal sem tohle
Hra se skládá z partií
dobry, mam urcite
Question 2
Body: 20
Jestliže ve hře vždy jeden hráč vyhraje a druhý prohraje nebo hra skončí remízou, pak
Vyberte alespoň jednu odpověď.
při bodování 1, -1, 0 jde o hru s konstantním součtem dal sem tohle
při bodování 1, 3, 2 jde o hru s nulovým součtem
při bodování 1, -1, 0 jde o hru s nulovým součtem dal sem tohle
při bodování 1, 3, 2 jde o hru s konstantním součtem
Question 3
Body: 20
Které z následujících tvrzení platí pro řešení hry dvou inteligentních hráčů s nulovým součtem?
Pokud jsou ve výplatní matici pouze záporné hodnoty, hra je nespravedlivá. dal T
Pokud existuje sedlový bod hry, vždy je možné ve výplatní matici nalézt pouze jeden. dal F
Pokud existuje řešení hry v oboru čistých strategií, dolní cena hry je menší než horní cena hry. dal F
Pokud jeden z hráčů zvolí pro řešení konfliktní situace jinou než svoji optimální čistou strategii, může dosáhnout lepšího výsledku než je horní cena hry. dal F
Pokud existuje sedlový bod hry, hra má řešení v oboru čistých strategií. dal T
Question 4
Body: 20
Určete dolní a horní cenu hry pro následující hru a rozhodněte o typu výsledku:
-10 10 -9 3
-1 10 2 8
0 -5 8 10
Dolní cena hry = dal -1
Horní cena hry = dal 10
Hra má řešení v oboru strategií. dal smisenych
z tohohle prikladu mam 13 b, tj. o 7 mene.
Question 5
Body: 20
Hráč má k dispozici 4 strategie. Řešením hry mohl dospět k následujícím doporučením. Přiřaďte jim správné označení.
„Hraj vždy strategii 2.“ dal cista
„Většinou hraj strategii 1, občas strategii 2, výjimečně strategii 3“ dal smisena
„Střídej strategie podle vektoru optimální strategie (0,5; 0,2; 0,1; 0,2)“ dal smisena
„Střídej strategie podle vektoru optimální strategie (0; 1; 0; 0)“ dal smisena
Z tohohle mam 82 b, zbyva nejasnych 11 b.
---
1
Body: 20
Strategie je
Vyberte jednu odpověď
chování hráče ve hře dal toto
cíl hráče
výplata hráče
jeden krok z chování hráče ve hře
Question 2
Body: 20
Hra s nulovým součtem je hra, ve které
Vyberte alespoň jednu odpověď.
oba mohou vyhrát i prohrát (ztratit i získat)
oba hráči získají stejnou výhru
jeden hráč získá to, co druhý ztratí dal jen toto
součet výher hráčů je proměnlivý
Question 3
Body: 20
Určete dolní a horní cenu hry pro následující hru a rozhodněte o typu výsledku:
5
2
-1
3
7
3
2
5
-1
-5
1
10
Dolní cena hry = 2
Horní cena hry = 2
Hra má řešení v oboru strategií. dal ciste
Question 4
Body: 20
Hráč má k dispozici 4 strategie. Kolik existuje různých smíšených strategií?
Vyberte jednu odpověď
Konečně mnoho, ale nelze to spočítat
Dvě
Nekonečné mnoho
Jedna
Čtyři............................................................dal tohle
Tři
asi tohle blbe
Question 5
Body: 20
Které z následujících tvrzení platí pro řešení hry dvou inteligentních hráčů s nulovým součtem?
Pokud jsou ve výplatní matici pouze záporné hodnoty, hra je nespravedlivá.
Pokud existuje sedlový bod hry, vždy je možné ve výplatní matici nalézt pouze jeden. ... dal T
Pokud existuje řešení hry v oboru čistých strategií, dolní cena hry je menší než horní cena hry.
Pokud jeden z hráčů zvolí pro řešení konfliktní situace jinou než svoji optimální čistou strategii, může dosáhnout lepšího výsledku než je horní cena hry.
Pokud existuje sedlový bod hry, hra má řešení v oboru čistých strategií.
bud tadyto blbe nebo uz nevim
/* z tohohle mam 76 */
----
1
Body: 20
Které z následujících tvrzení platí pro řešení hry dvou inteligentních hráčů s nulovým součtem?
Pokud existuje řešení hry v oboru čistých strategií, dolní cena hry se rovná horní ceně hry. dal T
Pokud jeden z hráčů zvolí pro řešení konfliktní situace jinou než svoji optimální čistou strategii, vždy dosáhne horšího výsledku, než by mohl. dal T
Pokud jsou ve výplatní matici pouze kladné hodnoty, hra je nespravedlivá. dal T
Pokud existuje sedlový bod hry, hra má řešení v oboru čistých strategií. dal T
Pokud existuje sedlový bod hry, vždy je možné ve výplatní matici nalézt pouze jeden. dal F
to mam asi ok
Question 2
Body: 20
Hra s konstantním součtem je hra, ve které
Vyberte alespoň jednu odpověď.
oba mohou vyhrát (získat)
součet výher je konstantní dal tohle
oba hráči získají stejnou výhru
jeden hráč získá to, co druhý ztratí dal tohle
asi je chyba tady, zrejme v te druhe polozce
Question 3
Body: 20
Aantagonistická hra je hra
Vyberte jednu odpověď
v níž vyhrávají všichni
nespravedlivá
spravedlivá
v níž vyhraje jen jeden dal tohle
to bude ok
Question 4
Body: 20
Hráč má k dispozici 4 strategie. Řešením hry mohl dospět k následujícím doporučením. Přiřaďte jim správné označení.
„Hraj vždy strategii 3.“ dal cista
„Střídej strategie podle vektoru optimální strategie (0; 0; 0; 1)“ dal smisena
„Většinou hraj strategii 2, občas zkus některou z ostatních“ dal smisena
„Střídej strategie podle vektoru optimální strategie (0,1; 0,1; 0,1; 0,7)“ dal smisena
mozno je chyba tady, ale spis ne
Question 5
Body: 20
Určete dolní a horní cenu hry pro následující hru a rozhodněte o typu výsledku:
-5 10 -10 3
-1 2 2 5
-1 -5 9 10
Dolní cena hry = dal -1
Horní cena hry = dal -1
Hra má řešení v oboru strategií. dal cistych
to je asi ok
/* z toho mam 95 b. :) */
----
1
Body: 20
Které z následujících tvrzení platí pro řešení hry dvou inteligentních hráčů s nulovým součtem?
Pokud jsou ve výplatní matici pouze kladné hodnoty, hra je nespravedlivá.
Pokud existuje řešení hry v oboru čistých strategií, dolní cena hry je menší než horní cena hry.
I když existuje sedlový bod hry, nemusí být reprezentován žádným polem ve výplatní matici. dal jsem F (snad dobre, nebo mozna blbe tohle)
Pokud jsou ve výplatní matici pouze kladné nebo záporné hodnoty, i přesto může být cena hry nulová. dal jsem F (asi blbe)
Pokud existuje sedlový bod hry, hra má řešení v oboru čistých strategií.
Question 2
Body: 20
Jestliže ve hře vždy jeden hráč vyhraje a druhý prohraje nebo hra skončí remízou, pak
Vyberte alespoň jednu odpověď.
při bodování 1, -1, 0 jde o hru s konstantním součtem dal jsem tohle
při bodování 1, 3, 2 jde o hru s nulovým součtem
při bodování 1, 3, 2 jde o hru s konstantním součtem
při bodování 1, -1, 0 jde o hru s nulovým součtem dal jsem tohle
ztratil jsem tim 5 b.
Question 3
Body: 20
Koalice (kooperace) je
Vyberte jednu odpověď
skupina neinteligentních hráčů
skupina inteligentních hráčů
skupina nespolupracujících hráčů
skupina spolupracujících hráčů dal jsem tohle
Question 4
Body: 20
Hráč má k dispozici 4 strategie. Kolik existuje různých smíšených strategií?
Vyberte jednu odpověď
Nekonečné mnoho
Dvě
Jedna
Čtyři
Tři dal jsem tohle (asi blbe)
Konečně mnoho, ale nelze to spočítat
Question 5
Body: 20
Určete dolní a horní cenu hry pro následující hru a rozhodněte o typu výsledku:
5 2 -1 3
0 3 2 5
-1 -5 1 2
Dolní cena hry =
Horní cena hry =
Hra má řešení v oboru strategií.
snad ok
/* z toho mam 63 b. */
---
3
Body: 20
Hráč má k dispozici 4 strategie. Kolik existuje různých čistých strategií?
Vyberte jednu odpověď
Jedna
Dvě
Nekonečné mnoho
Čtyři
Tři
Konečně mnoho, ale nelze to spočítat dal jsem tohle, ale bylo to blbe
---
Body: 20
Jestliže ve hře vždy jeden hráč vyhraje a druhý prohraje nebo hra skončí remízou, pak
Vyberte alespoň jednu odpověď.
při bodování 1, 3, 2 jde o hru s konstantním součtem dal jsem toto
při bodování 1, -1, 0 jde o hru s nulovým součtem dal jsem toto
při bodování 1, -1, 0 jde o hru s konstantním součtem dal jsem toto
při bodování 1, 3, 2 jde o hru s nulovým součtem
a mam 20 b.
----
1
Body: 20
Rozhodněte o pravdivosti tvrzení:
Model hry v normálním tvaru je reprezentován stromem hry.
Každá maticová hra je řešitelná, lze vždy najít optimální strategie hráčů a cenu hry.
Listy stromu hry představují výplaty hry pro dané kombinace strategií hráčů.
Model hry v rozvinutém tvaru je reprezentován výplatní maticí.
V jednotlivých hranách stromu hry volí hráči své tahy.
Uzly stromu hry zobrazují jednotlivé tahy ve hře.
Question 2
Body: 20
Určete dolní a horní cenu hry pro následující hru a rozhodněte o typu výsledku:
-5
10
-10
3
-1
2
2
5
-1
-5
9
10
Dolní cena hry =
Horní cena hry =
Hra má řešení v oboru strategií.
Question 4
Body: 20
V rozhodovacích situacích je hra definována jako
Vyberte jednu odpověď
konfliktní situace hráčů, kteří chtějí vyhrát tohle zaskrt, asi ok
oblíbená dětská činnost
ekonomický boj firem
hazardní hra
Question 5
Body: 20
Jestliže ve hře vždy jeden hráč vyhraje a druhý prohraje, pak
Vyberte alespoň jednu odpověď.
při bodování 1, 2 jde o hru s nekonstantním součtem
při bodování 1, -1 jde o hru s nekonstantním součtem
při bodování 1, 2 jde o hru s nenulovým součtem tohle zaskrt
při bodování 1, -1 jde o hru s nenulovým součtem
mam z toho dohroma 73 b.
----
4
Body: 20
Které z následujících tvrzení platí pro řešení hry dvou inteligentních hráčů s nulovým součtem?
Pokud existuje řešení hry v oboru čistých strategií, dolní cena hry se rovná horní ceně hry. dal T
Pokud existuje sedlový bod hry, hra nemá řešení v oboru čistých strategií. dal F
Pokud jsou ve výplatní matici pouze kladné nebo záporné hodnoty, žádná partie nemůže skončit remízou. dal F (asi blbe)
Pokud existuje sedlový bod hry, je někdy možné ve výplatní matici nalézt více sedlových bodů. nedal nic
a mam z toho 10 b., tj to treti bude T
----
2
Body: 20
Které z následujících tvrzení platí pro řešení hry dvou inteligentních hráčů s nulovým součtem?
atní matici pouze kladné nebo záporné hodnoty, žádná partie n. (spra T)
Pokud existuje sedlový bod hry, hra nemá řešení v oboru čistých strategií. (spra F)
Pokud jsou ve výplatní matici pouze kladné nebo záporné hodnoty, žádná partie nemůže skončit remízou. (spra T)
Pokud existuje sedlový bod hry, je někdy možné ve výplatní matici nalézt více sedlových bodů. (spra T)
Question 3
Body: 20
Hráč má k dispozici 4 strategie. Kolik existuje různých smíšených strategií?
Vyberte jednu odpověď
Čtyři
Konečně mnoho, ale nelze to spočítat
Dvě
Nekonečné mnoho.........................................toto je spra
Tři
Jedna
----
1
Hráč má k dispozici 4 strategie. Řešením hry mohl dospět k následujícím doporučením. Přiřaďte jim správné označení.
„Hraj vždy strategii 2.“ dal cist
„Většinou hraj strategii 1, občas strategii 2, výjimečně strategii 3“ dal smis
„Střídej strategie podle vektoru optimální strategie (0,5; 0,2; 0,1; 0,2)“ dal smis
„Střídej strategie podle vektoru optimální strategie (0; 1; 0; 0)“ dal smis
Question 2
Určete dolní a horní cenu hry pro následující hru a rozhodněte o typu výsledku:
1 -2 2 4
5 1 -1 1
-8 -5 -5 2
Dolní cena hry = dal -1
Horní cena hry = dal 1
Hra má řešení v oboru strategií. dal smis
Question 3
Body: 20
Jestliže ve hře vždy jeden hráč vyhraje a druhý prohraje, pak
Vyberte alespoň jednu odpověď.
při bodování 1, 2 jde o hru s konstantním součtem dal tohle
při bodování 1, -1 jde o hru s nulovým součtem dal tohle (njst, 5 b.)
při bodování 1, 2 jde o hru s nulovým součtem
při bodování 1, -1 jde o hru s konstantním součtem dal tohle
Question 4
Rozhodněte o pravdivosti tvrzení:
Listy stromu hry představují dílčí výplaty hry; pro stanovení optimální ceny hry je nutné tyto dílčí výsledky zprůměrovat. dal F (njst)
Model hry v rozvinutém tvaru je reprezentován stromem hry. dal T
Model hry v normálním tvaru je reprezentován výplatní maticí. dal T
Každá maticová hra je řešitelná, lze vždy najít optimální strategie hráčů a cenu hry. dal T
V jednotlivých hranách stromu hry volí hráči své tahy. dal T (njst)
Uzly stromu hry zobrazují jednotlivé tahy ve hře. dal T
Question 5
Tah je
Vyberte jednu odpověď
výplata hráče
jeden krok z chování hráče ve hře dal toto
chování hráče ve hře
cíl hráče
/* Z toho mam 88 b.*/
----
1
Body: 20
Které z následujících tvrzení platí pro řešení hry dvou inteligentních hráčů s nulovým součtem?
Pokud existuje řešení hry v oboru čistých strategií, dolní cena hry se rovná horní ceně hry. T
Pokud jeden z hráčů zvolí pro řešení konfliktní situace jinou než svoji optimální čistou strategii, vždy dosáhne horšího výsledku, než by mohl. T
Pokud existuje sedlový bod hry, hra nemá řešení v oboru čistých strategií. F
Pokud jsou ve výplatní matici pouze kladné hodnoty, hra je nespravedlivá. T
Pokud existuje sedlový bod hry, je reprezentován jedním nebo více poli ve výplatní matici. T
Question 2
Body: 20
Jestliže ve hře vždy jeden hráč vyhraje a druhý prohraje, pak
Vyberte alespoň jednu odpověď.
při bodování 1, 2 jde o hru s nenulovým součtem to sem dal
při bodování 1, -1 jde o hru s nekonstantním součtem
při bodování 1, 2 jde o hru s nekonstantním součtem to sem dal
při bodování 1, -1 jde o hru s nenulovým součtem
Question 3
Body: 20
V rozhodovacích situacích je hra definována jako
Vyberte jednu odpověď
hazardní hra
ekonomický boj firem
oblíbená dětská činnost
konfliktní situace hráčů, kteří chtějí vyhrát
Question 4
Body: 20
Určete dolní a horní cenu hry pro následující hru a rozhodněte o typu výsledku:
-5 10 -10 3
-1 2 2 5
-1 -5 9 10
Dolní cena hry = -1
Horní cena hry = -1
Hra má řešení v oboru strategií. cist
to je ok
Question 5
Body: 20
Hráč má k dispozici 4 strategie. Řešením hry mohl dospět k následujícím doporučením. Přiřaďte jim správné označení.
„Hraj vždy strategii 3.“
„Střídej strategie podle vektoru optimální strategie (0; 0; 0; 1)“
„Většinou hraj strategii 2, občas zkus některou z ostatních“ mozna blbe
„Střídej strategie podle vektoru optimální strategie (0,1; 0,1; 0,1; 0,7)“
/* z tohohle mam 75 */
---
Hráč má k dispozici 4 strategie. Řešením hry mohl dospět k následujícím doporučením. Přiřaďte jim správné označení.
„Hraj vždy strategii 2.“ ... dal jsem cista
„Většinou hraj strategii 1, občas strategii 2, výjimečně strategii 3“ dal jsem smisena
„Střídej strategie podle vektoru optimální strategie (0,5; 0,2; 0,1; 0,2)“ dal jsem smisena
„Střídej strategie podle vektoru optimální strategie (0; 1; 0; 0)“ dal jsem smisena
a mam 15 b., tj. to 2. bude taky cista
----
1
Body: 20
V rozhodovacích situacích je hra definována jako
Vyberte jednu odpověď
hazardní hra
ekonomický boj firem
konfliktní situace hráčů, kteří chtějí vyhrát to je spra
oblíbená dětská činnost
----
1
Body: 20
Které z následujících tvrzení platí pro řešení hry dvou inteligentních hráčů s nulovým součtem?
Pokud jsou ve výplatní matici pouze záporné hodnoty, hra je nespravedlivá.
Pokud existuje sedlový bod hry, vždy je možné ve výplatní matici nalézt pouze jeden.
Pokud existuje řešení hry v oboru čistých strategií, dolní cena hry je menší než horní cena hry.
Pokud jeden z hráčů zvolí pro řešení konfliktní situace jinou než svoji optimální čistou strategii, může dosáhnout lepšího výsledku než je horní cena hry.
Pokud existuje sedlový bod hry, hra má řešení v oboru čistých strategií.
Question 2
Body: 20
Hráč má k dispozici 4 strategie. Řešením hry mohl dospět k následujícím doporučením. Přiřaďte jim správné označení.
„Hraj vždy strategii 3.“
„Střídej strategie podle vektoru optimální strategie (0; 0; 0; 1)“
„Většinou hraj strategii 2, občas zkus některou z ostatních“
„Střídej strategie podle vektoru optimální strategie (0,1; 0,1; 0,1; 0,7)“
Question 3
Body: 20
Určete dolní a horní cenu hry pro následující hru a rozhodněte o typu výsledku:
10 -2 8 9
5 0 1 1
-8 -5 -5 10
Dolní cena hry =
Horní cena hry =
Hra má řešení v oboru strategií.
Question 4
Body: 20
Jestliže ve hře vždy jeden hráč vyhraje a druhý prohraje nebo hra skončí remízou, pak
Vyberte alespoň jednu odpověď.
při bodování 1, 3, 2 jde o hru s nekonstantním součtem
při bodování 1, -1, 0 jde o hru s nekonstantním součtem
při bodování 1, 3, 2 jde o hru s nenulovým součtem
při bodování 1, -1, 0 jde o hru s nenulovým součtem
Question 5
Body: 20
V nekooperativní hře nemůže být
Vyberte jednu odpověď
skupina nespolupracujících hráčů
skupina inteligentních hráčů
skupina spolupracujících hráčů
skupina neinteligentních hráčů
----
Jestliže ve hře vždy jeden hráč vyhraje a druhý prohraje, pak
Vyberte alespoň jednu odpověď.
při bodování 1, -1 jde o hru s nenulovým součtem
při bodování 1, 2 jde o hru s nekonstantním součtem
při bodování 1, 2 jde o hru s nenulovým součtem toto je spra
při bodování 1, -1 jde o hru s nekonstantním součtem
Lagrangeova funkce a Kuhn-Tuckerovy podmínky slouží pro řešení
Vyberte alespoň jednu odpověď.
nelineárních optimalizačních úloh dal
lineárních optimalizačních úloh dal dal
konvexních optimalizačních úloh dal
nekonvexních optimalizačních úloh dal dal dal
1. pokus 0 b, 2. pokus 0, 3. pokus 0 b.
----
Lagrangeova funkce převádí optimalizační úlohu na
Vyberte alespoň jednu odpověď.
problém hledání sedlového bodu funkce to je spra
úlohu na volný extrém
úlohu na vázaný extrém
pomocnou optimalizační úlohu
----
Úloha
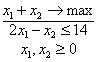 |
je
Vyberte jednu odpověď
jednokriteriální optimalizační úlohou to je spra
cílovou optimalizační úlohou
vícekriteriální optimalizační úlohou
----
Úloha
je
Vyberte alespoň jednu odpověď.
úlohou na vázaný extrém
optimalizační úlohou spra
úlohou na volný extrém
----
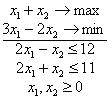 |
Úloha
je
Vyberte jednu odpověď
vícekriteriální optimalizační úlohou to je spra
cílovou optimalizační úlohou
jednokriteriální optimalizační úlohou
----
Účelová funkce v obecné optimalizační úloze zobrazuje
Vyberte alespoň jednu odpověď.
rozhodovací kritérium to je spra
sledované prvky, procesy
vazby mezi sledovanými prvky, procesy
----
Úloha
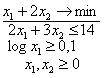 |
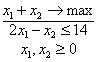 |
||
je
Vyberte jednu odpověď
jednokriteriální optimalizační úlohou to je spra
vícekriteriální optimalizační úlohou
cílovou optimalizační úlohou
---
Úloha
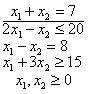 |
je
Vyberte jednu odpověď
vícekriteriální optimalizační úlohou
jednokriteriální optimalizační úlohou
cílovou optimalizační úlohou dal jsem tohle
----
Označte všechna pravdivá tvrzení
Vyberte alespoň jednu odpověď.
Úloha na volný extrém hledá extrém funkce za splnění omezujících podmínek. ... dal, spra
Úloha na volný extrém se nazývá úlohou nalezení extrému podél křivky.
Úloha na volný extrém hledá globální extrém funkce na části definičního oboru.
Úloha na volný extrém hledá globální extrém funkce (na celém definičním oboru). ... dal
A mám 0 b., správně je jen to první.
----
1)
Nelineární optimalizační model je formulován pomocí
Vyberte alespoň jednu odpověď.
alespoň jedné lineární funkce
alespoň jedné nelineární funkce dal jsem
pouze lineárních funkcí
2)
Úloha
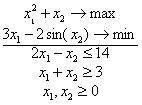 |
je
Vyberte jednu odpověď
vícekriteriální optimalizační úlohou dal jsem
cílovou optimalizační úlohou
jednokriteriální optimalizační úlohou
3)
Úloha
je
Vyberte alespoň jednu odpověď.
úlohou na vázaný extrém
úlohou na volný extrém dal jsem
optimalizační úlohou
A mám 20 b. :( A to bude z toho prvního příkladu.
---
Konvexní optimalizační model může být formulován pomocí
Vyberte alespoň jednu odpověď.
pouze lineárních funkcí
konvexní kriteriální funkce dal jsem
konvexní množiny přípustných řešení dal jsem
konvexní minimalizační funkce dal jsem
konkávní maximalizační funkce dal jsem
A mám 0 b.
---
Úloha
je
Vyberte alespoň jednu odpověď.
nekonvexní optimalizační úlohou
kvadratickou optimalizační úlohou dal jsem
nelineární optimalizační úlohou dal jsem
konvexní optimalizační úlohou dal jsem
lineární optimalizační úlohou
A mám 0 b.
---
Úloha
je
Vyberte alespoň jednu odpověď.
kvadratickou optimalizační úlohou
nekonvexní optimalizační úlohou
lineární optimalizační úlohou
nelineární optimalizační úlohou dal jsem
konvexní optimalizační úlohou
A mám 7 b.
---
Úloha
je
Vyberte alespoň jednu odpověď.
kvadratickou optimalizační úlohou
nekonvexní optimalizační úlohou dal jsem
konvexní optimalizační úlohou
lineární optimalizační úlohou dal jsem dal jsem
nelineární optimalizační úlohou
Z 1. pokusu mám 10 b, z 2. mám 0 b.
---
Úloha
je
Vyberte alespoň jednu odpověď.
kvadratickou optimalizační úlohou to je spra
lineární optimalizační úlohou
nelineární optimalizační úlohou to je spra
nekonvexní optimalizační úlohou
konvexní optimalizační úlohou to je spra
----
Úloha
je
Vyberte alespoň jednu odpověď.
úlohou na vázaný extrém
optimalizační úlohou
úlohou na volný extrém to je spra
---
Question 1
Body: 20
Zcela obecné postupy řešení neexistují pro
Vyberte alespoň jednu odpověď.
nekonvexní optimalizační úlohy dal jsem, je to spra
nelineární optimalizační úlohy nedal jsem, to je spra
konvexní optimalizační úlohy
lineární optimalizační úlohy
(správně je nekonvex a nelin, dal jsem jen to 1., proto jen 10 b.)
Question 2
Body: 20
Označte všechna pravdivá tvrzení
Vyberte alespoň jednu odpověď.
Úloha na vázaný extrém hledá globální extrém funkce na části definičního oboru. ... spra
Úloha na vázaný extrém se nazývá úlohou nalezení extrému podél křivky. ... dal, spra
Úloha na vázaný extrém hledá extrém funkce za splnění více omezujících podmínek.
Úloha na vázaný extrém hledá globální extrém funkce (na celém definičním oboru).
(správně je to druhé a to první, dal jsem jen to 2., proto jen 10 b.)
Question 3
Body: 20
Úloha
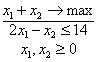 |
je
Vyberte jednu odpověď
cílovou optimalizační úlohou
vícekriteriální optimalizační úlohou
jednokriteriální optimalizační úlohou to je spra
Question 4
Body: 20
Úloha
je
Vyberte alespoň jednu odpověď.
konvexní optimalizační úlohou dal jsem
lineární optimalizační úlohou
nekonvexní optimalizační úlohou
nelineární optimalizační úlohou dal jsem
kvadratickou optimalizační úlohou dal jsem
Question 5
Body: 20
Z hlediska typu kritéria hovoříme o
Vyberte alespoň jednu odpověď.
modelu pro nalezeni lokálního či globálního extrému
minimalizačním, maximalizačním nebo cílovém modelu to je spra
volném či vázaném extrému.
jednokriteriálním nebo vícekriteriálním modelu
A mám 80 b.! :)
----
Obecné postupy řešení existují pro
Vyberte alespoň jednu odpověď.
konvexní optimalizační úlohy to je spra
lineární optimalizační úlohy to je spra
nekonvexní optimalizační úlohy
nelineární optimalizační úlohy
----
Označte všechna pravdivá tvrzení
Vyberte alespoň jednu odpověď.
Úloha na volný extrém hledá globální extrém funkce (na celém definičním oboru). dal
Úloha na volný extrém se nazývá úlohou nalezení extrému podél křivky.
Úloha na volný extrém hledá globální extrém funkce na části definičního oboru.
Úloha na volný extrém hledá extrém funkce za splnění omezujících podmínek. dal
A mám 0 b, bude to jen to první.
----
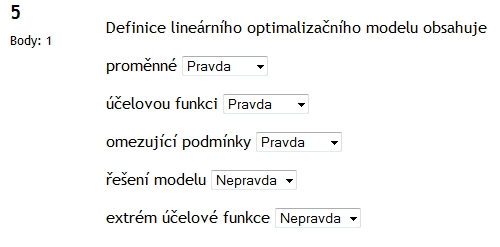
Vícekriteriální optimalizační model je model, který obsahuje
Vyberte alespoň jednu odpověď.
více proměnných to je spra
více účelových funkcí to je spra
více omezujících podmínek to je spra
jednu účelovou funkci
jednu proměnnou
jednu omezující podmínku
Z 1. pokusu mám 7 b, z 2. pokusu 0 b.
----
Question 2
Označte všechna pravdivá tvrzení
Vyberte alespoň jednu odpověď.
Úloha na volný extrém se nazývá úlohou nalezení extrému podél křivky.
Úloha na volný extrém hledá globální extrém funkce na části definičního oboru.
Úloha na volný extrém hledá extrém funkce za splnění omezujících podmínek.
Úloha na volný extrém hledá globální extrém funkce (na celém definičním oboru). dal
Question 3
Nekonvexní model je formulován pomocí
Vyberte alespoň jednu odpověď.
účelové funkce s více extrémy to je spra
nekonvexní množiny přípustných řešení dal jsem, to je spra
účelové funkce s jediným extrémem
konvexní množiny přípustných řešení
A mám 30 b. To první zřejmě za 20 b. a v tom 2. něco chybí.
----
Jednokriteriální optimalizační model je model, který obsahuje
Vyberte alespoň jednu odpověď.
více účelových funkcí
jednu účelovou funkci dal jsem
jednu proměnnou
více omezujících podmínek
více proměnných dal jsem
jednu omezující podmínku dal jsem
A mám 0 b.
----
Omezující podmínky v obecné optimalizační úloze zobrazují
Vyberte alespoň jednu odpověď.
vazby mezi sledovanými prvky, procesy to je spra
rozhodovací kritérium
sledované prvky, procesy
----
Question 1
Úloha
je
Vyberte alespoň jednu odpověď.
kvadratickou optimalizační úlohou dal jsem
lineární optimalizační úlohou
nelineární optimalizační úlohou dal jsem
nekonvexní optimalizační úlohou
konvexní optimalizační úlohou dal jsem
Question 2
Označte všechna pravdivá tvrzení
Vyberte alespoň jednu odpověď.
Obecná optimalizační úloha je naprosto odlišná od úlohy na vázaný extrém.
Obecná optimalizační úloha je naprosto odlišná od úlohy na volný extrém.
Obecná optimalizační úloha je totožná s úlohou na vázaný extrém.
Obecná optimalizační úloha vychází z úlohy na vázaný extrém. dal jsem
Obecná optimalizační úloha je totožná s úlohou na volný extrém.
Question 3
Zcela obecné postupy řešení neexistují pro
Vyberte alespoň jednu odpověď.
nelineární optimalizační úlohy to je spra
konvexní optimalizační úlohy
lineární optimalizační úlohy
nekonvexní optimalizační úlohy to je spra
Question 4
Úloha
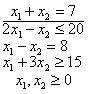 |
je
Vyberte jednu odpověď
vícekriteriální optimalizační úlohou
jednokriteriální optimalizační úlohou
cílovou optimalizační úlohou to je spra
Question 5
Nelineární optimalizační model je formulován pomocí
Vyberte alespoň jednu odpověď.
alespoň jedné lineární funkce
pouze lineárních funkcí
alespoň jedné nelineární funkce to je spra
A mám 80 b.
----
Kvadratický model je formulován pomocí
Vyberte alespoň jednu odpověď.
lineárních omezujících podmínek a libovolné kriteriální funkce
pouze lineárních funkcí
lineárních omezujících podmínek a kvadratické kriteriální funkce to je spra
pouze kvadratických funkcí
----
Obecná optimalizační úloha obsahuje
Vyberte alespoň jednu odpověď.
Omezující podmínky zobrazující sledované prvky, procesy
Proměnné zobrazující vazby mezi sledovanými prvky, procesy
Proměnné zobrazující sledované prvky, procesy to je spra
Omezující podmínky zobrazující vazby mezi sledovanými prvky, procesy to je spra
----
Úloha
je
Vyberte alespoň jednu odpověď.
konvexní optimalizační úlohou dal jsem
nelineární optimalizační úlohou dal jsem
nekonvexní optimalizační úlohou
lineární optimalizační úlohou
kvadratickou optimalizační úlohou
A mám z toho zřejmě 0 b.
----
Question 1
Úloha
je
Vyberte alespoň jednu odpověď.
nelineární optimalizační úlohou to je spra
konvexní optimalizační úlohou to je spra
kvadratickou optimalizační úlohou to je spra
lineární optimalizační úlohou
nekonvexní optimalizační úlohou
Question 2
Body: 20
Obecné postupy řešení existují pro
Vyberte alespoň jednu odpověď.
lineární optimalizační úlohy to je spra
nelineární optimalizační úlohy
nekonvexní optimalizační úlohy
konvexní optimalizační úlohy to je spra
Question 3
Úloha
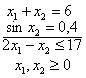 |
je
Vyberte jednu odpověď
vícekriteriální optimalizační úlohou
jednokriteriální optimalizační úlohou
cílovou optimalizační úlohou to je spra
Question 4
Označte všechna pravdivá tvrzení
Vyberte alespoň jednu odpověď.
Obecná optimalizační úloha má vždy jen jednu omezující podmínku.
Obecná optimalizační úloha mívá více omezujících podmínek než úloha na vázaný extrém. to je spra
Obecná optimalizační úloha mívá více proměnných než úloha na vázaný extrém.
Obecná optimalizační úloha má vždy jen jednu proměnnou.
(možná, že tady by mohlo být zaškrtnuto ještě to třetí)
Question 5
Vícekriteriální optimalizační model je model, který obsahuje
Vyberte alespoň jednu odpověď.
více proměnných dal jsem
více omezujících podmínek dal jsem
jednu omezující podmínku
jednu účelovou funkci
jednu proměnnou
více účelových funkcí dal jsem
A mám z toho 90 b.!
----
Question 1
Úloha
je
Vyberte alespoň jednu odpověď.
konvexní optimalizační úlohou dal jsem
nekonvexní optimalizační úlohou
nelineární optimalizační úlohou
kvadratickou optimalizační úlohou
lineární optimalizační úlohou dal jsem, mělo by být spra
Question 2
Označte všechna pravdivá tvrzení
Vyberte alespoň jednu odpověď.
Obecná optimalizační úloha vychází z úlohy na vázaný extrém.
Obecná optimalizační úloha je totožná s úlohou na volný extrém.
Obecná optimalizační úloha je naprosto odlišná od úlohy na vázaný extrém. dal jsem
Obecná optimalizační úloha je totožná s úlohou na vázaný extrém.
Obecná optimalizační úloha je naprosto odlišná od úlohy na volný extrém. dal jsem
A mám z toho dohroma 20 b.
----
Lineární optimalizační model je formulován pomocí
Vyberte alespoň jednu odpověď.
alespoň jedné lineární funkce
alespoň jedné nelineární funkce
pouze lineárních funkcí to je spra
----
Body: 0
Označte všechna pravdivá tvrzení
Vyberte alespoň jednu odpověď.
|
|
Obecná optimalizační úloha je totožná s úlohou na volný extrém. |
|
|
|
Obecná optimalizační úloha je totožná s úlohou na vázaný extrém. |
|
|
|
Obecná optimalizační úloha vychází z úlohy na vázaný extrém. |
|
|
|
Obecná optimalizační úloha je naprosto odlišná od úlohy na volný extrém. |
|
|
|
Obecná optimalizační úloha je naprosto odlišná od úlohy na vázaný extrém. |
|
Body: 20
Proměnné v obecné optimalizační úloze zobrazují
Vyberte alespoň jednu odpověď.
|
|
vazby mezi sledovanými prvky, procesy |
|
|
|
rozhodovací kritérium |
|
|
|
sledované prvky, procesy |
|
Body: 20
Omezující podmínky v obecné optimalizační úloze zobrazují
Vyberte alespoň jednu odpověď.
|
|
sledované prvky, procesy |
|
|
|
rozhodovací kritérium |
|
|
|
vazby mezi sledovanými prvky, procesy |
|
Úloha
![]()
Body: 0
Vyberte alespoň jednu odpověď.
|
|
nekonvexní optimalizační úlohou |
|
|
|
konvexní optimalizační úlohou |
|
|
|
nelineární optimalizační úlohou |
|
|
|
lineární optimalizační úlohou |
|
|
|
kvadratickou optimalizační úlohou |
|
Body: 0
Vyberte alespoň jednu odpověď.
|
|
konvexní optimalizační úlohou |
|
|
|
nelineární optimalizační úlohou |
|
|
|
nekonvexní optimalizační úlohou |
|
|
|
lineární optimalizační úlohou |
|
|
|
kvadratickou optimalizační úlohou |
|
Body: 0
Vyberte alespoň jednu odpověď.
|
|
lineární optimalizační úlohou |
|
|
|
nekonvexní optimalizační úlohou |
|
|
|
konvexní optimalizační úlohou |
|
|
|
kvadratickou optimalizační úlohou |
|
|
|
nelineární optimalizační úlohou |
|
Body: 0
Vyberte alespoň jednu odpověď.
|
|
lineární optimalizační úlohou |
|
|
|
konvexní optimalizační úlohou |
|
|
|
nelineární optimalizační úlohou |
|
|
|
kvadratickou optimalizační úlohou |
|
|
|
nekonvexní optimalizační úlohou |
|
Úloha
![]()
Body: 0
Vyberte alespoň jednu odpověď.
|
|
nelineární optimalizační úlohou |
|
|
|
kvadratickou optimalizační úlohou |
|
|
|
nekonvexní optimalizační úlohou |
|
|
|
konvexní optimalizační úlohou |
|
|
|
lineární optimalizační úlohou |
|
Úloha
![]()
Body: 20
Vyberte alespoň jednu odpověď.
|
|
lineární optimalizační úlohou |
|
|
|
konvexní optimalizační úlohou |
|
|
|
nelineární optimalizační úlohou |
|
|
|
kvadratickou optimalizační úlohou |
|
|
|
nekonvexní optimalizační úlohou |
|
Body: 0
Heuristické metody řešení optimalizačních úloh
Vyberte alespoň jednu odpověď.
|
|
porovnávají všechna řešení |
|
|
|
porovnávají náhodně vybraná přípustná řešení |
|
|
|
vyhledávají optimální řešení |
|
|
|
porovnávají náhodně vybraná nepřípustná řešení |
|
Body: 20
Řešit optimalizační model obsahuje následující úlohy
Vyberte alespoň jednu odpověď.
|
|
Najít přípustná řešení |
|
|
|
Najít nepřípustná řešení |
|
|
|
Najít body extrému účelové funkce |
|
|
|
Najít vhodnou grafickou reprezentaci modelu |
|
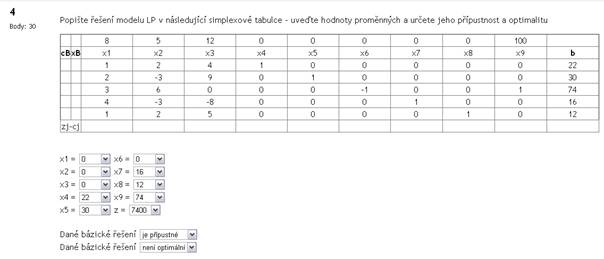
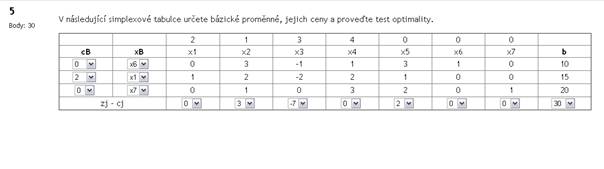
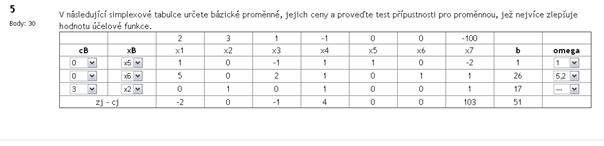







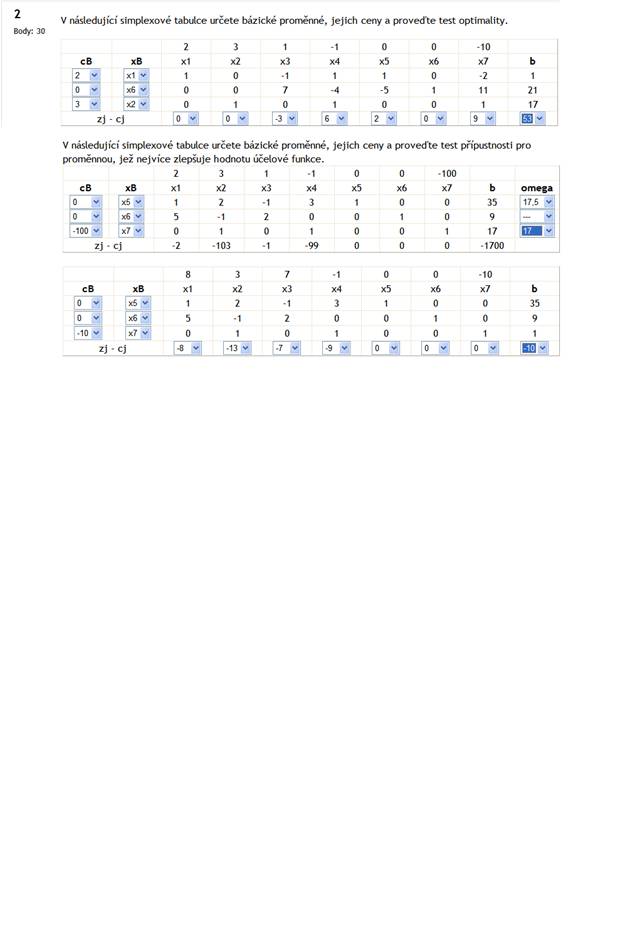



Pro řešitelnost modelu lineárního programování platí:
|
Pokud existuje optimální řešení modelu lineárního programování, obvykle se nachází na hranici množiny přípustných řešení, ve výjimečných případech mimo ni (uvnitř). |
|
Pokud je množina omezujících podmínek nekonzistentní, model nemá přípustné řešení. |
|
Pokud je množina přípustných řešení reprezentována otevřenou konvexní množinou, má model lineárního programování nekonečně mnoho optimálních řešení. |
|
Pokud je množina přípustných řešení reprezentována konvexním polyedrem, potom má model lineárního programování vždy právě jedno optimální řešení. |
Označte všechna správná tvrzení:
|
Hodnoty bázických proměnných v bázickém řešení odpovídají příslušným hodnotám z vektoru pravých stran. |
|
Hodnotu účelové funkce v bázickém řešení nelze určit, protože neznáme všechny hodnoty proměnných. |
|
Nebázické proměnné považujeme za parametry, a proto jejich hodnoty můžeme libovolně volit. |
|
Nebázická proměnná má ve svém sloupci v matici soustavy jednotkový vektor. |
|
Hodnoty nebázických proměnných v bázickém řešení pokládáme rovny nule. |
Vyberte alespoň jednu odpověď:
|
Suboptimální řešení není zároveň nikdy přípustné. |
|
Přípustné řešení vyhovuje omezujícím podmínkám a hodnota jeho účelové funkce je nulová. |
|
Alternativní řešení je zároveň vždy degenerované. |
|
Přípustné řešení vyhovuje všem omezujícím podmínkám, ale hodnota jeho účelové funkce nemusí být optimální. |
|
Optimální řešení musí být vždy přípustné. |
Pro interpretaci grafu s řešením modelu lineárního programování platí:
|
Pokud není možné z grafu prostým způsobem odečíst souřadnice hodnot proměnných v optimálním řešení, musí se získat jako řešení soustavy dvou rovnic o dvou neznámých. |
|
Pokud je přímka účelové funkce rovnoběžná s některou z hran konvexního polyedru, model může mít nekonečně mnoho optimálních řešení. |
|
Hodnota účelové funkce optimálního řešení se určí dosazením předem získaných hodnot proměnných do jejího předpisu. |
|
Pokud bod optima leží na hraniční přímce omezující podmínky, potom je tato omezující podmínka splněna jako nerovnice. |
|
Pokud není množina přípustných řešení uzavřena, nelze nikdy najít optimální řešení s konečnou hodnotou účelové funkce. |
Příklad:
Na místě musí být tolik policistů (p), aby minámlně pokryli počet demonstrantů (d) (1:1), a aby ještě dalších 25 policistů zbylo pro ochranu objektu.
|
p = d + 25 |
|
|
d = p + 25 |
|
|
p <= d + 25 |
|
|
p >= d + 25 |
|
|
p - d >= 25 |
|
3) Systémová analýza, operační výzkum, modely a modelování
Model: model je záměrně zjednodušený obraz skutečnosti vytvořený pomocí zvolených zobrazovacích prostředků.
a) Operační analýza
Cílem operačního výzkumu je poskytnout exaktní systémové informace pro řešení problémů ve složitých systémech.
Optimalizační modely
- slouží k nalezení nejlepšího řešení problémů,
- možná řešení jsou prvky nějaké konečné či nekonečné množiny
- např. lineární, nelineární, dynamické, stochastické programování nebo vícekriteriální rozhodování
Distribuční a dopravní modely
- slouží k řešení problémů spojených s dopravou či distribucí
Modely plánování a řízení projektů
- modely umožňující časovou, nákladovou a zdrojovou analýzu projektů, ve kterých probíhá více operací, které jsou na sobě závislé
- cílem je zajistit nejvýhodnější průběh těchto operací
Modele teorie rozvrhování
- cílem je najít nejvýhodnější časové a prostorové uspořádání průmyslových operací z mnoha různých hledisek
Modely strukturální analýzy
- bilancují vztahy mezi jednotlivými hospodářskými odvětvími vyhledávají rovnovážný stav systému
- modely Leontijevovy
Simulační modely
- speciální typ modelů, které popisují a napodobují strukturu a chování zkoumaných objektů
- např. hromadné obsluhy, zásob, obnovy a marketingové modely
Stochastické modely
- poskytují informace o systémech s náhodným chováním
Teorie rozhodování a teorie her
- zabývá se popisem a řešení konfliktních situací, kdy důsledky rozhodnutí jsou závislé nejen na rozhodnutí samotném, ale i na dalších faktorech.
4) Teorie rozhodování
- Rozhodovací proces je charakterizován jako proces volby nejvýhodnějšího rozhodnutí z několika možných alternativ rozhodnutí.
- Riziko spojené s výběrem určité alternativy rozhodnutí chápáno jako možnost nežádoucích výsledků, ke kterým by vedla realizace zvolené alternativ za nepříznivých situací.
- Nejistotu můžeme chápat jako nemožnost spolehlivého stanovení budoucích hodnot faktorů ovlivňujících dopady a účinky volby variant.
Vlastnosti rozhodovacího modelu
Rozhodovací situace je charakterizována jako proces volby z alespoň dvou možných variant – alternativ rozhodnutí.
Volba rozhodnutí závisí na možných alternativách rozhodnutí a jejich vlastnostech, na faktorech, které ovlivňují výsledky rozhodnutí, a na vlastnostech těchto faktorů a především na cíli a kritériu rozhodování.
Alternativy a stavy okolností
Možná rozhodnutí pro řešení problému se nazývají alternativami. Alternativy se navzájem musí vylučovat.
Stavy okolností jsou situace, které ovlivňují výsledky jednotlivých alternativ. Stejně jako alternativy se musí vzájemně vylučovat.
Výplatní tabulka
Každá alternativa za odpovídajícího stavu okolností je ohodnocena výsledkem, kterým je určitý hospodářský efekt. Tento efekt se nazývá výplatou.
Výplatní nebo rozhodovací tabulkou se nazývá matice rozměru m x n (jestliže je m alternativ a n stavů okolností), jejímiž prvky jsou jednotlivé výplaty.
Rozhodovací tabulky jsou maticovou formou rozhodovacího modelu. Rozhodovací modely mohou mít též grafickou formu – rozhodovací strom. O nich ale bude pojednáno dále v souvislosti s pravděpodobnostními stromy.
Rozhodovací kritérium
Při volbě se řídíme záměrem a přístupem rozhodovatele k problému.
Jistota a riziko
Důležitým rysem rozhodovací situace pravděpodobnosti pj je realizace jednotlivých stavů okolností. Vektor těchto pravděpodobností p je často nazýván vektorem rizika.
Pokud je rozhodovateli známo, jaký stav okolností nastane, rozhoduje za podmínek jistoty.
Jestliže musí rozhodovat za podmínek úplné nejistoty, rozhodovatel nemá vůbec žádnou představu o tom, jaký bude aktuální stav okolností.
Situace ležící mezi těmito dvěma krajními možnostmi, kdy rozhodovatel sice neví s jistotou, jaký bude aktuální stav okolností, ale na základě různých poznatků a zpráv soudí, který stav okolností to pravděpodobně bude. Může se ovšem mýlit. Pak rozhoduje za podmínek rizika. Riziko je tím větší, čím menší je pravděpodobnost realizace určitého stavu okolností a naopak.
Pro hodnoty p. ve vektoru rizika platí:
1) rozhodování s jistotou: pravděpodobnost pj známého stavu okolností J je rovna 1 a pravděpodobnosti pj ostatních stavů okolností jsou rovny 0
2) rozhodování s rizikem: pro pravděpodobnosti pj realizace stavů okolností platí 0<pj<1 a suma pj = 1
3) rozhodování za nejistoty: pravděpodobnosti pj realizace stavů okolností jsou neznámé
Objektivní a subjektivní pravděpodobnosti
Objektivní p. jsou určovány na základě minulých statistických údajů, jsou stanoveny vždy číselně
Subjektivní p. vyjadřuje míru toho, že jen nastane, na základě osobního přesvědčení rozhodovatele, jsou buď číselné nebo slovní
Možnosti řešení rozhodovacích modelů
Cílem těchto modelů je určení takové alternativy rozhodnutí v závislosti na jednotlivých výplatách, která poskytne rozhodovateli nejlepší výsledek.
Tři základní skupiny metod pro analýzu a řešení:
- volba dominantní alternativy
- volba nejvýhodnější alternativy
- volba alternativy rozhodnutí podle nejvyššího užitku
Dominance alternativ
Dominance neboli převaha jedné alternativy nad druhou je vztahem mezi dvěma alternativami, které definuje jednu z alternativ jako lepší a druhou alternativu jako horší.
Nejsilnější formou dominance je dominance podle výplat, slabší je dominance podle stavů okolností a nejslabší je dominance podle pravděpodobnosti. Dominance podle výplat implikuje dominanci podle stavů okolností a ta implikuje dominanci podle pravděpodobností.
Dominance podle výplat
Je založena na požadavku, aby dominující alternativa poskytovala všechny výplaty lepší nebo stejně dobré jako alternativa dominovaná, aby nejhorší výplata dominující alternativy byla lepší nebo stejná jako nejlepší výplata alternativy dominované. Ve vícekriteriálních variantách tato volba není možná.
Dominance podle stavu okolností
Je založena na požadavku, aby dominující alternativa poskytovala pro každý stav okolností výplaty lepší nebo stejné jako alternativa dominovaná.
Dominance podle pravděpodobností
Pravděpodobnosti hodnot výplat stejných nebo lepších než nějaká hodnota x jsou u dominující alternativy větší nebo stejné jako u alternativy dominované.
Tato forma dominance je založena na kumulativní pravděpodobnosti hodnot výplat. Kumulativní pravděpodobnosti P (v ij >= x) lze vypočítat pro hodnoty výplat v ij a danou hodnotu x podle vztahu
Graf kumulativní pravděpodobnosti P (v ij >= x) je nazýván profil rizika. Poskytuje globální pohled na velikost výplat a odpovídá na otázky
- s jakou pravděpodobností dosáhnout jednotlivé alternativy určité hodnoty výplat? (lze vypočítat dosazením aspirační úrovně)
- jakou minimální výplatu je možné očekávat u jednotlivých alternativ s danou pravděpodobností.
Nejvýhodnější alternativa
Nejvýhodnější alternativa je chápána jako alternativa slibující nejlepší výplatu.
Nejvýhodnější alternativa při rozhodování za jistoty
Kdyby rozhodovatel získal spolehlivou informaci o tom, který stav okolností bude aktuální v bodě realizace jeho rozhodnutí a pokud by tedy takovou informaci rozhodovatel znal, rozhodoval by za podmínek jistoty = zvolil by tu alternativu, která má pro daný stav okolností nejlepší výplatu.
Pokud tedy při rozhodování známe stav okolností sj a jedná-li se o maximalizační kritérium, nejvýhodnější alternativa je vybrána podle vztahu:
Nejvýhodnější alternativa při rozhodování za úplné nejistoty
Pro výběr rozhodnutí řada postupů, při nichž jsou hodnoceny buď výplaty nebo ztráty jednotlivých alternativ a které se liší mírou rozhodovatelova optimismu či pesimismu.
a) maximaxový přístup
- použijeme ho v případě, že „odvážnému štěstí přeje“ a rozhodovatel je tedy ochoten riskovat
- řešením je alternativa, která přinese nejlepší výplatu
- za účelem nalezení maximální výplaty vyhledává rozhodovatel maximální výplatu pro každou alternativu a z nich vybere opět maximum.
b) maximinový přístup (Waldovo kritérium)
- „lepší něco než nic“
- rozhodovatel vybírá mezi nevýhodnými výplatami, aby si z nich vybral tu nejméně špatnou
- podle tohoto kritéria je tedy situace posuzována z hlediska nejhorších možných výsledků
- rozhodovatel nejprve vyhledává minimální výplatu pro každou alternativu a z nich vybere výplatu maximální
c) princip minimaxové ztráty (Savageovo kritérium)
Předchozí mají nevýhodu, že se fixují na jednu určitou výplatu a nepřihlížejí k výplatám ostatním. Je rozumné posuzovat alternativy podle toho, kolik je možno při jednotlivých stavech okolností ztratit vzhledem k nejlepší výplatě, je-li vybrána jiná než alternativa s nejlepší výplatou. Jedná se o použití Waldova kritéria pro matici ztrát.
Při uplatňování minimaxové ztráty se v každém sloupci matice vyhledají maximální výplaty při maximalizačním rozhodovacím kritériu a od těch se odečtou ostatní výplaty ve sloupci.
Pro jednotlivé alternativy se pak určí maximální ztráty. Jako optimum se pak vybírá alternativa a1, která odpovídá minimální z maximálních ztrát. Pro maximalizační kritérium platí
d) princip nedostatečné evidence (Bernoulli-Laplaceův princip)
Tento přístup se snaží zohlednit všechny výplaty a jednotlivé stavy okolností považuje za stejně pravděpodobné tj. rozhodování za podmínek nejistoty je převedeno na rozhodování za podmínek rizika s pravděpodobnostním vektorem s hodnotami
Ohodnocení jednotlivých alternativ je dáno váženým součtem výplat, který je v tomto případě ekvivalentní jejich průměru. Jako nejvýhodnější alternativa se vybírá ta, která vede k nejlepšímu průměrnému výsledku. Tento princip leze použít pro výplatní matici i pro matici ztrát. Při maximalizačním typu výplat i kritéria bude podle výplat vybrána alternativa a1, pro kterou platí
e) Hurwiczovo kritérium
Je založeno na očekávání nejlepších a nejhorších výsledků každé z alternativ. Nejprve je třeba stanovit tzv. optimisticko pesimistický index t pro který platí 0<= t <= 1.
Tento index vyjadřuje očekávaný podíl nejlepší a nejhorší výplaty každé varianty. Hodnota t je mírou optimismu rozhodovatele a hodnota 1 – t je mírou jeho pesimismu.
Dále se vypočítá optimismem a pesimisme vážený průměr nejlepších a nejhorších výplat pro každou strategii.
Nejvýhodnější alternativa při rozhodování za rizika
Předpokládá znalost vektoru rizika (informace o pravděpodobnostech realizace jednotlivých stavů okolností). Vektor označíme p = (p1, p2, p3………. pn)T pro jeho složky platí:
a) očekávaná hodnota výplaty
- používáme Bayerův princip: používáme pro volbu optimální varianty tzv. očekávané hodnoty a pomocí nich se odhadují důsledky rozhodnutí (volíme alternativu s nejlepší očekávanou - střední výplatou, resp. nejnižší očekávanou – střední ztrátou bez ohledu na jednotlivé výplaty).
- očekávaná hodnota výplaty (EMV) představuje vážený aritmetický průměr výplat odpovídajících každé alternativě, kde vahami jsou pravděpodobnosti každého stavu okolností
- pokud se jedná o maximalizaci, bude vybrána alternativa s maximální EMV, tedy
b) očekávaná možná ztráta
Očekávaná možná ztráta (EOL) představuje vážený aritmetický průměr ztrát odpovídajících každé alternativě, kde vahami jsou pravděpodobnosti každého stavu okolností. Podle tohoto pravidla bude vybrána alternativa s minimální EOL, tedy
Princip očekávané možné ztráty vede ke stejnému výsledku jako princip očekávané výplaty.
c) pravděpodobnost dosažení aspirační úrovně
Jinou možností je porovnávání pravděpodobností, s nimiž jednotlivé alternativy budou poskytovat alespoň určitou hodnotu výplaty. Nejvýhodnější alternativa je v tomto případě vybírána podle pravděpodobnosti toho, že její výplata bude lepší než požadovaná úroveň výplat α.
Dodatečné informace
Rozhodování probíhá zřídka za podmínek jistoty i za podmínek úplné nejistoty. Skoro vždy se jedná o rozhodování za rizika. Podstata obtížnosti problému spočívá v tom, že za situace rizika rozhodovatel neví, jaký stav okolností nastane. Disponuje pouze odhady pravděpodobností jejich realizace. Proto si snaží opatřit dodatečné informace, které by potvrdily jeho odhady, případně doplnily jeho informace tak, aby se riziko snížilo, resp. rozhodnutí za rizika se přiblížilo rozhodnutí za jistoty.
Získání těchto informaci: výběrové šetření, předpovědní techniky (jsou však spojeny s dodatečnými náklady).
a) očekávaná hodnota spolehlivé informace (EVPI)
Každá dodatečná informace je spojena s dodatečnými náklady. Proto bude rozhodovatel uvažovat o tom, zda se dodatečné náklady vyplatí. Posouzení jejich účelnosti se provádí porovnáním očekávané hodnoty výplaty,jak je definována pro rozhodování za rizika s očekávanou hodnotou výplaty, jaká by byla dosažena při rozhodování za jistoty, za jednotlivých stavů okolností.
EVPI je definována jako rozdíl očekávané hodnoty výplaty za podmínek jistoty EPC (je definována jako vážený aritmetický průměr nejlepších výplat pro každý stav okolností, kde vahou jsou pravděpodobnosti jejich realizace tedy) a nejvyšší očekávané hodnoty výplaty za podmínek rizika EMV, tedy
Hodnota EVPI se plně shoduje s nejnižší očekávanou hodnotu možné ztráty EOL.
Alternativy výpočtu EVPI:
- jako rozdíl očekávané výplaty za jistoty EPC a nejvyšší očekávané výplaty za rizika EMV
- jako nejnižší očekávaná hodnota možné ztráty EOL.
EVPI umožňuje rozhodovateli posoudit výhodnost resp. nevýhodnost eventuálního dodatečného výběrového šetření za účelem oslabení rizika.
b) očekávaná hodnota výběrové informace
Efektivnost nákladů na výběrové informace se vyjadřuje rozdílem očekávané hodnoty výplaty při uplatnění dodatečné výběrové informace a očekávané hodnoty výplaty bez jejího uplatnění, např. s použitím původního vektoru rizika. Očekávaná hodnota výplaty bez dodatečné informace pro jednotlivé alternativy je hodnota EMV.
Dodatečná výběrová informace je pak představována zpřesněným vektorem rizika např. na základě výběrových šetření. Očekávaná hodnota výplaty při dodatečné výběrové informace EMVS se vypočítá jako
Očekávaná hodnota výběrové informace EVSI je potom rozdíl EVSI = EMVS – EMV (pokud je tento rozdíl výrazně větší než jsou náklady na pořízení dodatečné výběrové informace, je EVSI výhodná)
Někdy se pro posouzení velikosti EVSI formalizuje také ukazatel Ф, nazývaný efektivnost výběrové informace. Ten vyjadřuje srovnání EVSI k očekávané hodnotě spolehlivé informace, resp. k očekávané hodnotě výplaty za jistoty.
Hodnota tohoto poměru se blíží nule při malé efektivnosti a jedné při vysoké efektivnosti výběrové informace.
Postup řešení:
1) nejprve se ověří spolehlivost prováděných odhadů
2) ve sloupcích tabulky musí být součty pravděpodobností rovny jedné
3) pro ověření vhodnosti nového výzkumu se použije složená pravděpodobnost na základě empirie a odhadu jednotlivých stavů
4) tyto ověřené pravděpodobnosti současně umožňují stanovit revidované pravděpodobnosti pro skutečné úrovně poptávky pro všechny možné případy
5) sestaví se doplněný rozhodovací strom, ve kterém jsou zobrazeny výsledky rozhodnutí pro všechny varianty všech rozhodnutí a možných stavů okolností
Rozhodovací stromy
Rozhodovací model může mít maticovou formu, nebo může mít formu grafickou, formu rozhodovacího stromu. Rozhodovací stromy popisují průběh rozhodovací situace pomocí prostředků teorie grafů, pomocí stromů. Rozhodovací stromy obsahují uzly a hrany zobrazující postup rozhodování.
- ukazují, jaké další důsledky a kombinace okolností mohou nastat, zvolíme-li určitou cestu
- nutí promýšlet každou variantu do všech důsledků
- hledají faktory nejistoty pro jednotlivé varianty
Rozhodovací problém je možno zobrazit pomocí grafu, který nazýváme rozhodovací strom. Uzly rozhodovacího stromu se rozlišují na uzly rozhodovací a situační. Hrany se pak dělí na hrany vystupující z rozhodovacích uzlů, které zobrazují alternativy a ze situačních uzlů, které zobrazují stavy okolností. Výplatami v ij pro příslušnou kombinaci alternativa/stav okolností jsou ohodnoceny listy rozhodovacího stromu.
Kořenem rozhodovacího stromu je rozhodovací uzel R, který odpovídá okamžiku rozhodnutí (je ve čtverečku). Na něj navazují hrany jednotlivých alternativ, představující rozhodnutí. Situační (možnostní) uzel M pak odpovídá okamžiku realizace vybrané alternativy ovlivněné jedním ze stavů okolností (je v kroužku). Listy rozhodovacího stromu představují výsledek rozhodovací situace, jsou ohodnoceny výplatami. (rozhodovací tabulky volí situace izolovaně)
Předností stromu je především dodatečné přidání následných rozhodnutí. Následným rozhodnutím míníme opatření rozhodovatele pro případ, že by se realizoval nepříznivý stav okolností. Tato dodatečná rozhodnutí korigují zvolené alternativy tak, aby se zvýšily výplaty. Je rozumné, aby rozhodovatel byl připraven na možná dodatečná rozhodnutí.
Pravděpodobnostní stromy
Pravděpodobnostní stromy představují grafický nástroj pro výpočet důsledků jednotlivých rizikových rozhodnutí, skládajících se z jednotlivých kroků.
Pravděpodobnostní strom zobrazuje průběh realizace rizikového rozhodnutí. Uzly pravděpodobnostního stromu zobrazují jednotlivé kroky rozhodnutí jejichž výsledek je ovlivňován rizikem. Hrany prav. stromu, vycházející z těchto uzlů, zobrazují možné výsledky těchto rizikových kroků včetně jejich pravděpodobností. Listy pravděpodobnostního stromu představují možná ukončení rozhodnutí a jsou ohodnoceny důsledky jednotlivých rizikových kroků.
Slouží k ohodnocení výsledků jediného postupu, který je ovlivňován několika rizikovými faktory, není ho možné použít k jinému modelu (jako rozhodovací strom).
Výhodou prav. stromu je především jednoduchost zobrazení poměrně složitých alternativ rozhodnutí, která jsou posloupnostmi kroků zatížených rizikem. Tyto pravděpodobnosti se vypočítají jako násobky pravděpodobnostního ohodnocení hran ležících na větvi vedoucí z kořenového uzlu do příslušného listu pravděpodobnostního stromu. Nevýhodou je možnost zobrazit pouze diskrétní rizikové faktory jako např. prodáno či neprodáno. Pokud je rizikový faktor spojitý, jako např. velikost poptávky po zboží, je třeba ho aproximovat několika málo hodnotami, např. velká, střední, malá, žádná.
5) Matematické programování
Obecný optimalizační model
Při použití optimalizačních modelů musí být matematicky formulována omezení.
Rozhodnutí, řešení resp. hodnoty jeho prvků či procesů je popsáno vektorem proměnných
x = (x1, x2 , … xn )T ε R n
jehož každá složka vyjadřuje rozsah jednoho procesu, aktivity či prvku rozhodnutí. Možné řešení je omezeno podmínkami, které určují varianty rozhodnutí. Tyto omezující podmínky jsou vyjádřeny vhodnými funkcemi a rovnicemi nebo nerovnicemi, …
Množinou přípustných řešení nazýváme množinu
každý prvek x množiny M nazýváme přípustným řešením. Vektory x, které nesplňují omezující podmínky se nazývají nepřípustným řešením.
Cíl, podle něhož je vybíráno rozhodnutí, je popsán funkcí, která se nazývá účelová nebo kriteriální funkce. Kritériem rozhodnutí je nejčastěji optimalizace výsledku, tedy nalezení maximální nebo minimální hodnoty funkce f (x). Potom se jedná o maximalizační resp. minimalizační model.
Řešení x opt, které splňuje omezující podmínky a v němž účelová funkce nabývá svého optima, resp. maxima se nazývá optimální řešení.
Řešení suboptimálním x sub, tj. řešením které je z hlediska kritéria velmi dobré, účelová funkce v něm nabývá velmi dobré hodnoty, ale nedosahuje své minimální nebo maximální hodnoty.
Klasifikace optimalizačních modelů
Jednokriteriální o.m. : jediné kritérium
Vícekriteriální o.m. : více kritérií (není vždy možno hledat řešení problému pouze z jednoho hlediska)
Z hlediska typu kritéria:
- minimalizační model: jde o nalezení minimální hodnoty účelové funkce
- maximalizační model: jde o nalezení maximální hodnoty účelová funkce.
- cíle modelu (úlohu) : kdy je kritériem rozhodnutí dosažení předem daného výsledku – cíle
Podle typu použitých funkcí se optimalizační modely dělí na
- lineární optimalizační modely: které ve své formulaci využívají pouze lineární funkce a jsou obecně řešitelné simplexovým algoritmem
- nelineární optimalizační modely: v jejichž matematickém popisu je alespoň jedna nelineární funkce
Nelineární modely dále dělíme na
- konvexní modely
- nekonvexní modely
6) Lineární programování
Cílem modelu lineárního programování jakožto optimalizačního modelu je nalézt řešení splňující omezující podmínky, v němž kriteriální funkce nabývá požadovaného extrému. V případě lineárního modelu jsou omezující podmínky vyjádřeny pomocí lineárních rovnic a nerovnic a kritérium pomocí lineární funkce.
Grafické řešení úlohy LP
Prostor řešení: prostor, ve kterém leží všechny přípustná řešení problému. Zobrazujeme zde jak množinu přípustných řešení tak vhodným způsobem účelovou funkci a její chování.
Množina přípustných řešení úlohy LP vznikne jako průnik poloprostorů tj. konvexní množina. Pokud je omezená jedná se o konvexní polyedr. Pokud je neomezená vznikne polyedrický kužel.
Řešení potom nalezneme na přímce zobrazující účelovou funkce ve směru růstu nebo poklesu její hodnoty, která má s množinou přípustných řešení alespoň jeden společný bod. Takový bod je vždy na hranici množiny přípustných řešení (ve vrcholu nebo hraně). Souřadnice těchto bodů jsou hledané hodnoty proměnných optimálního řešení. Optimální hodnota účelové funkce se získá dosazením optimálních hodnot proměnných.
Řešitelnost:
1) množina přípustných řešení je prázdná: omezující podmínky jsou nekonzistentní a model nemá řešení
2) množina p.ř. je konvexní polyedr: lineární optimalizační model má optimální řešení
a. jediné řešení, pokud poslední průsečík přímky účelové fce s množinou přípustných řešení je vrchol polyedru
b. nekonečně mnoho řešení: pokud je tento průsečík hranou či stěnou polydru
3) množina p.ř. je neomezená, je polyedrický kužel: množina v jednom směru nabývá libovolně velkých nebo malých hodnot
Prostor požadavků: je prostor, ve kterém je možno zobrazit vektory koeficientů jednotlivých proměnných (nazývají se aktivity) a vektor pravých stran omezujících podmínek (nazývá se požadavek). Nalezení množiny je chápáno jako skládání vhodných vektorů, tak aby výsledek této operace byl právě vektor pravých stran.
Simplexový algoritmus
Simplexová metoda je nejznámější univerzální metoda pro řešení úloh lineárního programování. Je to metoda iterační, která využívá Jordanovu eliminační metodu doplněnou o dvě kritéria umožňující nalézt optimální řešení.
Jordanova eliminační metoda
Jordanova metoda tedy vede k úpravě soustavy lineárních rovnic do kanonického tvaru.
Povolené eliminační úpravy soustavy rovnice
1) násobení řídící rovnice převrácenou hodnotou řídícího prvku
2) přičtením vhodného násobku řídící rovnice k upravované rovnici
Bazické, nebazické a parametrické řešení
Je-li soustava lineárních rovnic o n proměnných převedena do kanonického tvaru, pak kanonické proměnné, jejichž koeficienty vytvářejí jednotkovou matici, nazýváme bazické proměnné. Všechny ostatní proměnné nazýváme nebázické proměnné. Každé bazické řešení obsahuje nejvýše m nenulových složek.
Bazickým (základním) řešením soustavy lineárních rovnic nazýváme takový vektor x, jehož nenulové složky odpovídají bazickým vektorům.
Degenerované řešení úlohy LP je takové, kde alespoň jedna z bazických proměnných má nulovou hodnotu. Degenerované řešení tedy obsahuje více jak (n-m) nulových složek. Nedegenerované řešení obsahuje právě (n-m) nulových složek.
Pokud budeme považovat hodnoty nebázických proměnných za parametry, dostaneme parametrické řešení soustavy lineárních rovnic, ve kterém jsou vyjádřeny hodnoty bazických proměnných pomocí parametrů – hodnot nebázických proměnných.
Pokud za nebázické proměnné položíme určité hodnoty, dostaneme konkrétní hodnoty i pro bázické proměnné. Takové řešení je nebázické nebo nezákladní.
Matice transformace
Inverzní matici k dané regulární čtvercové matici B označíme B -1 platí pro ně B x B -1 = B x B -1 = E
Matice transformace B -1 je inverzní maticí k matici báze B.
Kritérium optimality řešení: je založeno na zjišťování, zda lze k danému řešení x p soustavy omezujících podmínek najít řešení jiné, které bude mít lepší hodnotu kritéria – účelové funkce.
Alternativní optimální řešení se nazývá takové optimální řešení, které není jediné.
Kritérium přípustnosti
některou z nebázických proměnných x k se nyní pokusíme zařadit místo některé z bazických proměnných x r, kterou z řešení vyloučíme. Přitom chceme, aby nové řešení v bázi B bylo opět nezáporné a hodnota účelové funkce byla lepší.
Simplexový algoritmus vyžaduje lineární optimalizační model s omezujícími podmínkami v rovnicovém tvaru, kanonickém tvaru a s nezápornými hodnotami pravých stran, vektor b. Z tohoto tvaru soustavy omezujících podmínek se určí výchozí bázické řešení.
Dále se provede test optimality. Pokud jsou hodnoty (z – c) rovny nule, výpočet končí, nalezení řešení je optimální. Pokud je kriteriální hodnota záporná, vybere se proměnná x, která má být do báze zařazena. Potom se přejde k testu přípustnosti. Přechod na nové bázické řešení potom vyžaduje provést jeden krok Jordanovy eliminační metody podle vybraného prvku. Dále opět test optimality nového řešení.
Protože simplexová metoda umožňuje řešit pouze úlohy lineárního programování s omezujícími podmínkami v rovnicovém tvaru, v kanonickém tvaru a s nezápornými hodnotami vektoru pravých stran, je třeba každý model do tohoto tvaru transformovat. Nezápornost pravých stran zajistíme vynásobením -1.
Transformace do rovnicového tvaru je založena na myšlence uměle rozšířit počet proměnných modelu tak, aby nové proměnné vytvořily požadovaný kanonický rovnicový tvar soustavy omezujících podmínek
Omezující podmínka lineárního modelu je nerovnice typu <= (>=). Jedná se o kapacitní podmínku, která může být převedena do kanonického tvaru doplněním nezáporné proměnné, jejímž cílem je vyrovnat rozdíl pravé a levé strany podmínky (nezáporné proměnné vyjadřující překročení požadavku). Nazývá se doplňková proměnná typu rezerva (překročení).
Omezující podmínka lineárního modelu je rovnice, ale není v kanonickém tvaru. Tyto podmínky je nutné rozšířit o pomocné proměnné, které pomáhají vytvořit kanonický tvar.
Koeficienty c j v účelové funkci obecně vyjadřují přínos jednotkové proměnné k hodnotě účelové funkce. Nevyužité výrobní zdroje nebo překročení požadavků hodnotu produkce zvýší, proto se oceňují nulovou cenou.
Vyjádření pomocných proměnných z výpočtu docílíme tím, že koeficienty pomocných proměnných v účelové funkci budou velmi nevýhodné. Nazýváme je prohibitivní sazbou (cenou).
Optimální rozhodnutí závisí také na kvalitativních vlivech, které nelze popsat lineární optimalizační modelem. V důsledku vzájemných vlivů modelovaného systému a jeho okolí nebo v důsledku působení náhodných činitelů. Postoptimalizační analýza umožňuje stanovit rozsah přípustných změn v rámci kterých nedochází ke změně optimálního řešení a jak postupovat při vyhledávání nového optimálního řešení.
Matici transformace nalezneme v těch sloupcích výsledné tabulky, v nichž ve výchozí tabulce byly jednotkové vektory
Duální hodnoty pro strukturní proměnné udávají, o kolik se zhorší hodnota účelové funkce, zařadíme-li jednotku daného procesu do řešení, nebo pro doplňkové proměnné udávají, oč se zhorší hodnota účelové funkce, necháme-li jednotku daného činitele nevyužitou.
Alternativní řešení je z hlediska hodnoty účelové funkce řešením optimálním. Získá se zařazením nebázické proměnné s nulovou duální hodnotu (zj – cj) = 0 do řešení, tj. volbou nezáporné hodnoty této nebázické proměnné.
Suboptimální řešení získáme jestliže alespoň jedné z nebázických proměnných x j přiřadíme nenulovou hodnotu. Duální hodnota této nebázické proměnné (zj – cj ) je bližší nule.
Pokud s zabýváme pouze jednou nebázickou proměnnou xk, řešení zůstane přípustné, jestliže požadovaná hodnota splňuje podmínku x k náleží (0, ). Tento interval nazýváme intervalem přípustných hodnot proměnné x k.
Analýza citlivosti se zabývá určováním takového rozsahu změn výchozích údajů LO úlohy, v rámci kterých nedochází ke změně optimální báze.
8) Vícekriteriání optimalizační modely
Modely vícektriteriálního rozhodování (VR) zobrazují rozhodovací problémy, v nichž se důsledky rozhodnutí posuzují podle více kritérií. Zohlednění vícekritérií při hodnocení vnáší do řešení problémů obtíže. Účelem modelů těchto situacích je buĎ nalezení „nejlepší“ varianty podle všech uvažovaných hledisek, vyloučení neefektivních variant nebo uspořádání množiny variant. Přístupy k VR se liší podle charakteru množiny variant či přípustných řešení. Podle způsobu jejího zadávání lze rozlišit dvě skupiny těchto modelů.
- Modely vícekriteriálního hodnocení variant jsou zadány pomocí konečného seznamu variant a jejich ohodnocení podle jednotlivých kritérií.
- Modely vícekriteriální optimalizace mají množinu variant s nekonečně mnoho prvky vyjádřenou pomocí omezujících podmínek a ohodnocení jednotlivých variant je dáno jednotlivými kriteriálními funkcemi.
Vícekriteriální lineární programování
= úloha vektorové optimalizace
Jedná se o modely, které mají množinu variant vyjádřenou soustavou omezujících podmínek a množinu kritérií vyjádřenou kriteriálními funkcemi. Cílem je nalezení požadovaného extrému těchto kritérií na množině přípustných řešení.
Základním pojmem teorie VP je pojem dominované a nedominované řešení.
Jsou-li x i a x j dvě přípustná řešení, potom říkáme, že řešení x i dominuje řešení x j, jestliže platí
Cx i >= Cx j. Přípustné řešení x i je nedominovaným (efektivním) řešením úlohy, pokud neexistuje žádné jiné přípustné řešení, které by jej dominovalo.
Ideální řešení je hypotetické nebo reální řešení, reprezentované ve všech kritériích současně nejlepšími možnými hodnotami.
Bazální řešení je hypotetické nebo reální řešení, reprezentované nejhorším ohodnocením podle všech kritérií.
Kompromisní řešení je řešení, které má od ideálního řešení nejmenší vzdálenost podle vhodné metriky.
Prvky lineárního vícekriteriálího optimalizačního modelu
1) vektor proměnných x, který popisuje jednotlivé složky hledaného rozhodnutí
2) omezující podmínky, které popisují reálná omezení hledaných rozhodnutí
3) vektor účelových nebo kriteriálních funkcí, který popisuje cíle, kritéria hledaného rozhodnutí
Metody řešení úlohy VO
Uživatel si přeje získat výsledek, který má odpovídat různým požadavkům a zároveň je pro ně j konečným rozhodnutím. (závisí především na preferencích uživatele).
Zadání preferencí:
- zadání cílových hodnot kritérií
- forma uspořádání kritérií od nejdůležitějšího k……
- zadáním vah kritérií ohodnocující důležitost kritéria
Pro řešení vícekriteriální optimalizační úlohy existuje řada různých přístupů (metod) lišících se především povahou informace požadované od řešitele, kvalitou poskytovaného výsledku nebo postupem výpočtu.
1) dílčí optimalizace
2) agregace do jediné globální kriteriální funkce, tím se vícekriteriální úloha převádí na klasickou úlohu s jedinou účelovou funkcí
3) zajištění požadované úrovně kritéria formou jeho převodu na omezující podmíku
4) cílovým programováním – pro každou uvažovanou kriteriální fci se předem zadává požadovaná cílová úroveň, které by měla dosáhnout. Smyslem je vyhledat takové kompromisní řešení, které se k této úrovni co nejvíc blíží,
5) interaktivní iterační metody – založeny jsou na dialogu mezi vyhodnocovatelem a řešitelem.
Dílčí optimalizace řešením VO rozumíme řešení, které splňuje všechny omezující podmínky a optimalizuje jedno z kritérií modelu (řešíme tak p jednokriteriáních optimalizačních modelů). Význam je především analytický neboŤ umožňují hodnotit vliv jednotlivých kritérií na výsledek řešení problému, resp. jejich výsledky slouží jako východiska pro jiné metod yVP. Pro každé toto řešení můžeme určit hodnoty všech kritéríí z kj a tyto údaje zapsat do čtvercové kriteriální matice.
Na diagonále leží ideální řešení (nejlepší možné hodnoty kritéri). Bazální řešení je pak charakterizované nejhoršími hodnotami kritérií v jednotlivých sloupcích tabulky.
Agregace kriteriální funkce znamená sloučit všechny kritéria pomocí vhodného operátoru do kritéria jediného. Použitý operátor by měl zajistit, aby žádné kritérium nebylo jeho prostřednictvím zkresleno a nechtěně zvýrazněno či zeslabeno. Základní formy agregace kritérií jsou součinová či podílová a součtová či rozdílová. Příslušnými operátory jsou součin, kriteriálních funkcí nebo jejich součet atd. Pokud jsou všechna kritéria stejného typu, jedná se o jejich součin nebo součet, podíl (rozdíl) se používá jsou-li různého typu.
Operátorem agregace je konvexní lineární kombinace kritérií. Při této formě agregace předpokládáme, že uvažovaná kritéria mají přidelené váhy v i vyjadřující stupeň důležitosti. Jsou z intervalu <0,1>, Váhové koeficienty lze normovat na základě vztahu suma v k = 1. Potom se mluví o normovaných vahách a příslušná lineární kombinace kritérií je konvexní.
Úprava kriteriálních fcí na omezující podmínky: kteroukoliv omezující podmínku lze formulovat jako kriteriální funkci a naopak. Požadavek maximalizace kritéria tak lze formulovat jako požadavkovou podmínku (dosažení alespoň požadované hodnoty kritéria), požadavek minimalizace kritéria lze chápat jako kapacitní podmínku (nepřekročení určité hodnoty kritéria).
Princip tohoto způsobu řešení vychází z následující úvahy. Mějme úlohu VO se dvěma kritériálními funkcemi f1 a f2, u obou funkcí hledáme maximum…..(viz strana 104)
Řešením původní úlohy rozšířené o nové podmínky získáme hledané kompromisní řešení, nebo zjistíme, že požadavky na hodnoty kritérií nejsou splnitelné. S požadovanými hodnotami kritérií lze v obou uvedených postupech experimentovat.
Cílové programování
Vycházíme z výpočtu kompromisního řešení rozšířeného o minimalizaci odchylek od cílových (žádoucích) hodnot jednotlivých kritérií zadaných uživatelem. Vstupními údaji nejsou ovšem pouze cílové hodnoty kritérií. Uživatel dále musí určit preference dosažení jednotlivých cílových hodnot. Tyto preference mohou být vyjádřeny dvěma základními způsoby:
- splnění cílů resp. odchylky od cílových hodnot, lze ohodnotit pomocí vah, přiřazených jednotlivých kriteriálním funkcím. Čím vyšší je důležitost přiblížení se k danému cíli, tím bude zřejmě vyšší váhový koeficient u záporné či kladné diference. Vážený součet odchylek pak vytváří nové optimalizační kritérium, jehož minimalizací lze získat kompromisní řešení.
- vyjádření preferencí jednotlivých kritérií pomocí jejich pořadí na základě jejich důležitosti. Takový model se pak řeší lexikografickou metodou
Modely cílového programování obsahují speciální druh proměnných. Jsou to umělé odchylkové proměnné, představující odchylky od předem stanovených cílových hodnot v kladném nebo záporném směru. Proměnné překročení vyjadřují odchylky v kladném směru, kladné diference a udávají, o kolik je skutečná hodnota daného kritéria vyšší než hodnota cílová d +. V opačném případě jde o proměnné nedosažení, vyjadřující záporné diference d -.
Interaktivní postupy
Interační postupy jsou založeny právě na dialogu mezi rozhodovatelem a řešitelem, přičemž výměna informací probíhá v řadě iterací. Na počátku postupu řešitel vypočte a sdělí rozhodovateli výchozí přibližné řešení. Rozhodovatel pak předá řešiteli informace, na jejichž základě vypočte řešitel zpřesněné řešení a to opět sdělí rozhodovateli. Celý postup se opakuje tak dlouho, dokud se nedojde k řešení, které je ochoten rozhodovatel přijmout.
Metoda ALOP: je založena na principu prohledávání množiny hodnot kriteriálních fcí, nabízí uživateli směry postupu, které on může, ale nemusí akceptovat
Metoda STEM: metoda je použitelná pro situace, které umožňují kompenzaci hodnot kritérií, tj. dostatečné zlepšení hodnoty jednoho kritéria vyváží zhoršení hodnoty jiného kritéria.
9) Vícekriteriální analýza variant
Na rozdíl od VO či VP je v model vícekriteriálího hodnocení variant množina variant zadána ve formě konečného seznamu variant, které jsou ohodnoceny podle jednotlivých kritérií. Toto hodnocení může mít dvě základní formy – ohodnocení ordinální nebo kardinální.
Účelem modelových výpočtů je buď nalezení „nejlepší“ varianty podle všech uvažovaných hledisek vyloučením neefektivních variant nebo stanovení preferenčního pořadí variant z hlediska celého soubor kritérií, přičemž první varianta v tomto pořadí je varianta kompromisní.
Kritéria rozeznáváme maximalizační (čím vyšší hodnota, tím lepší hodnocení) a minimalizační. Celkové hodnocení variant závisí jednak na důležitosti (preferencích) jednotlivých kritérií (interkriteriální preference), jednak na hodnocení variant – alternativ podle jednotlivých kritérií (intrakriteriální preference).
Typy informací o důležitosti kritérií:
1) žádná informace – preferenční informace neexistují
2) nominální informace – i toto je informace přípustná pouze pro preference kritérií mezi sebou – je vyjádřena pomocí aspiračních úrovní tj. nejhorších možných hodnot, při nichž může být varianta akceptována a rozděluje varianty na akceptovatelné a neakceptovatelné
3) ordinální informace – vyjadřuje uspořádání kritérií podle důležitosti nebo uspořádání variant podle toho, jak jsou hodnoceny kritériem
4) kardinální informace – má kvantitativní charakter, v případě preference kritérií se jedná o váhy, v případě ohodnocení variant podle kritéria o konkrétní číselné vyjádření tohoto ohodnocení.
Dominovaná varianta: předpokládejme všechna kritéria maximalizační. Varianta ai dominuje variantu a j, jestliže platí (y i1, y i2..) >= (y j1, y j2….) a existuje alespoň jedno kritérium f l, že y il > y jl.
Paretovská varianta: varianta, která není dominována žádnou jinou variantou, je nedominovaná varianta, často se též nazývá efektivní nebo paretovská. Množina všech nedominovaných variant označíme A N. Množina řešení, o které nelze rozhodnout, které z nich je horší, ale víme, že nelze nalézt lepší.
Ideální varianta je hypotetická nebo reálná varianta, která obsahuje ve všech kritériích současně nejlepší možné hodnoty.
Bazální řešení je hypotetická nebo reálná varianta, jejíž ohodnocení je nejhorší podle všech kritérií.
Kompromisní varianta je řešení, které má od ideální varianta nejmenší vzdálenost podle vhodné metriky. (je jediná varianta doporučená jako řešení problému)
Metody řešení modelů vícekriteriální analýzy variant (VAV) se liší podle typů vstupních informací – modelových dat.
Preference kritérií – informace o důležitosti jednotlivých kritérií
alternativy rozhodnutí – možná rozhodnutí
Kvantifikace ordinální informace
Metoda pořadí
je-li známa ordinální informace – pořadí variant. Nejlepší variantu ohodnotíme číslem p (= počet variant), druhou nejlepší číslem p – 1, atd. Pokud bude několik ohodnocení stejných, pak tyto varianty ohodnotíme průměrným pořadím. Takto kvantifikované kritérium je potom maximalizační. Pokud bychom chtěli kritérium minimalizační, bude ohodnocení varianta postupovat od čísla 1 k p. K určení vah – přísutp několika expertů. Každý z nich seřadí kritéria, nejlepšímu přiřadí k (= počet kritéríí). Sečteme všechny body a vydělíme je celkovým počtem bodů od všech expertů. Suma vah = 1.
Bodovací metoda
stanovíme bodovou stupnici. Smí se používat i desetinná čísla a více variantám je možné přiřadit stejnou bodovou hodnotu. Při maximalizačním typu ohodnocení je varianta ohodnocena tím větším počtem bodů, čím lépe je ohodnocena.
Také tato metoda se pro výpočet vah kritérií používá tehdy, hodnotí-li ji více expertů.
Metoda párového porovnávání
Pokud předpokládáme, že uživatel ohodnotí prvek x jako důležitější než y a zároveň prvek y jako méně důležitý než x, stačí provést počet srovnání.
k (k – 1)
N = ------------------
2
k je počet porovnávaných prvků.
Toto porovnávání se většinou provádí pomocí tzv. Fullerova trojúhelníku.
Saatyho metoda (kvantitativního porovnávání)
Tato metoda slouží k určení vah kritérií, hodnotí-li je pouze jeden expert. Jde o metodu kvantitativního párového porovnávání kritérií. Při vytváření párových srovnání se používá 9-ti bodová stupnice. (1 – rovnocenná kritéria, 3 – slabě preferované kritérium i před j, 5 – silně.., 7 – velmi silně, 9 – absolutně preferované kritérium i před j)
Export porovná každou dvojici kritérií a velikosti preferencí i-tého kritéria vzhledem k j-tému kritérium zapíše do Saatyho matice S. Jsou-li i-té a j-té kritérium rovnocenná, je s ij = 1, preferuje-li slabě i-té kritérium před j-tým je s ij = 3……….
Metody řešení modelů
Bodovací metoda a metoda pořadí
Metoda aspiračních úrovní
Tato metoda je použitelná, je-li známa nominální informace o kritériích, tedy nejhorší přípustné hodnoty kritérií, a kardinální ohodnocení variant podle jednotlivých kritérií.
- konjunktivní metody : připustíme pouze varianty, které splňují všechny aspirační úrovně
- disjunktivní metody : připustíme varianty, které splňují alespoň jeden požadavek
Jsou-li požadavky vyjádřené aspiračními úrovněmi příliš vysoké, přísné, bude množina akceptovatelných variant prázdná. V takovém případě je nutno snížit požadavky, uvolnit požadované aspirační úrovně.
Metoda váženého součtu
vyžadují kardinální informace, kriteriání matici Y a vektor vah kritérií v. Obě konstruují celkové hodnocení pro každou variantu, a tak je leze použít jak pro hledání jedné nejvýhodnější varianty, tak pro uspořádání variant od nejlepší po nejhorší.
Vychází z principu maximalizace užitku. Dosáhne-li varianta ai podle kritéria f j určité hodnoty y ij, přináší tak uživateli určitý užitek, který lze vyjádřit pomocí funkční hodnoty dílčí funkce užitku uj (yij). Funkční hodnoty užitku leží v intervalu <0,1> a čím je varianta výhodnější, tím je vyšší hodnota užitku.
10) Distribuční a dopravní úlohy
distribuční modely pomáhají řešit základní otázky přemíšťování či přiřazování lidí, materiálu a informací, které lze vyjádřit slovy odkud, kam, čím a kudy.
Typy distribučních modelů:
distribuční modely jsou speciálním případem lineárních optimalizačních modelů. Odlišují se speciálními typem matice A, ve které se vyskytuje velice málo nenulových často jednotkových koeficientů.
Mezi klasické distribuční modely patří dopravní modely, jejichž cílem je nalézt optimální způsob přepravy materiálu, zboží apod. Důležitý je počet stupňů přepravy tj. počet míst, meziskladů, přes které je přeprava realizována a počet indexů, tj. počet rozlišovaných způsobů přepravy – dopravních prostředků.
Jednostupňová dopravní úloha
Cílem tohoto modelu je najít takový plán přepravy mezi m dodavateli a n spotřebiteli, při kterém budou celkové přepravní náklady minimální a budou vyčerpány kapacity dodavatelů a uspokojeny požadavky spotřebitelů.
dodavatelé a jejich kapacity
spotřebitelé a jejich požadavky
dopravní náklady – ohodnocení každé trasy dodavatel – spotřebitel
Řešitelnost dopravní úlohy
Dvě podmínky řešitelnosti dopravního problému – úplná zastupitelnost přepravovaného produktu a dělitelnost materiálu a vyváženost úlohy (všichni dodavatelé dohromady musí být schopni uspokojit všechny požadavky spotřebitelů a nic nesmí přebývat a nic nesmí chybět tj. součet kapacit dodavatelů se musí rovnat součtu požadavků spotřebitelů).
Jsou-li tyto dvě podmínky splněny, omezující podmínky dopravní úlohy jsou soustavou lineárních rovnic, které splňuje Frobeniovu větu, a proto jsou řešitelné.
Vyváženost dopravní úlohy
úlohy, ve kterých se součet kapacit rovná součtu požadavků, se nazývají vyvážené, a úlohy, ve kterých se součet kapacit nerovná součtu požadavků, se nazývají nevyvážené dopravní úlohy.
Nevyváženost může znamenat buď přebytek kapacit dodavatelů nebo převis požadavků spotřebitelů.
Převis požadavků spotřebitelů znamená, že kapacity dodavatelů jsou menší než požadavky spotřebitelů… rozšíříme o fiktivního dodavatele. Doplňkové proměnné x vyjadřují zásobování spotřebitelů od fiktivního neexistujícího dodavatele, tedy množství, které spotřebitelé nedostanou. Ceny za tuto přepravu jsou nulové. Pokud je nutno některého spotřebitele skutečně plně zásobit, pak bude použita prohibitivní cena.
Přebytečnou kapacitu, která dodavatelům zůstane ve skladu nahradíme fiktivním spotřebitelem. Ceny jsou opět nulové.
Řešení
algoritmus řešení DÚ
1) nalezení výchozího bazického přípustného řešení pomocí tzv. aproximačních metod:
- metody severozápadního rohu
- indexové metody
- Voglovy aproximační metody
2) test optimality ukáže, zda je možno nalézt jiné základní řešení s lepší hodnotou účelové funkce
3) přechod k lepšímu řešení pomocí tzv. Dantzigových uzavřených obvodů představuje změnu báze, jestliže testované řešení nebylo optimální
Výchozí bázické řešení
Nalezení výchozího bazického řešení je tedy založeno pouze na vhodném výběru tras, kterými se bude nějaké množství přepravovat. Je nutné vybírat trasy s nejmenšími náklady. Omezující podmínky dopravního modelu jsou lineárně závislé, jakmile však jednu vynecháme, zbývající jsou již lineárně nezávislé. Počet bazických proměnných v řešení této soustavy je tedy roven m + n – 1.
Metoda severozápadního rohu
1) v dopravní tabulce vybereme neobsazené volné pole, které má nejnižší možné indexy (severozápadní polev tabulce … tj x 11)
2) vybrané proměnné přiřadíme hodnotu maximálního možného převáženého množství zboží, upravíme kapacity a požadavky
3) dodavatele nebo spotřebitele s vyčerpanou kapacitou či požadavkem vyškrtneme
Indexová metoda
postup se liší pouze při výběru první trasy………nejprve obsahuji volné pole, které má nejnižší sazbu
Vogelova aproximační metoda
Poskytuje řešení velmi blízká řešení optimálnímu. Pro obsazení určité trasy od dodavatele je důležitá relativní výhodnost vzhledem k možnému zvýšení dopravních nákladů, pokud nebude možno využít trasu nejlevnější.
Relativní výhodnost každé trasy se zjišťuje pomocí rozdílu mezi nejvýhodnější a druhou nejvýhodnější sazbou tras od dodavatele (v řádku) reps.ke spotřebiteli (ve sloupci). Tyto rozdíly lze interpretovat jako minimální velikost možné jednotkové ztráty, která by vznikla, kdybychom obsadili nikoli nejvýhodnější, ale až druhé nejvýhodnější pole
1) vypočtou se diference mezi nejvýhodnější a druhou nejvýhodnější sazbou (při minimalizaci mezi nejnižší a druhou nejnižší sazbou)
2) určí se maximální diference, ve vybraném řádku nebo sloupci se vybere trasa s nejvýhodnější sazbou (při stejných maximálních diferencích – obsazuje přednostně pole s nejvýhodnější sazbou z hlediska všech sazeb v matici sazeb – sedlové pole, několik sedlových polí – přednostně obsazujeme to pole, pro které je součet řádkových a sloupcových diferencí maximální)
Dantzigovy uzavřené obvody
představují grafické schéma v distribuční tabulce, které naznačuje jak provést úpravy řešení, jak přesunout převážené zboží z jedné trasy na jinou a přitom nebyly porušeny podmínky dopravní úlohy, tj. velikost kapacit a požadavků.
Dantzigovy uzavřené obvody jsou grafickým znázorněním lineární závislosti proměnných, resp. jejich vektorů koeficientů v omezujících podmínkách dopravního modelu.
Dantzigův uzavřený obvod je uzavřená posloupnost – cyklus na sebe navazujících tras, která obsahuje v řešení již použité trasy a právě jednu trasu novou, jejíž každé dvě sousední trasy mají vždy buď stejného dodavatele nebo stejného spotřebitele.
Množství převáženého materiálu trasami ležícími na uzavřeném obvodu označujeme střídavě znaménky + a -. Nová trasa, resp. množství převáženého materiálu touto trasou bude označeno +, protože touto trasou plánujeme novou přepravu a tedy se bude hodnota proměnné zvyšovat. Chceme-li aby nové řešení bylo bazické, musíme tedy touto trasou převážet maximální možné množství zboží, tedy minimální z hodnot x ij (je transport novou trasou) příslušných trasám, které se nacházejí ve vrcholech uzavřeného obvodu označených znaménkem -.
Test optimality
je založen na porovnání sazeb jednotlivých nebázických tras c rs a příslušných nepřímých sazeb z rs, tj. na porovnání hodnoty skutečných dopravních nákladů touto trasou a nákladů ekvivalentní tras, pomocí níž je materiál přepravován………..
Přepravu trasou x rs nazveme přímou přepravou a cena kombinací přeprav, která je ekvivalentní přepravě od dodavatele ke spotřebiteli. … z rs – c rs <= 0 tato podmínky se nazývá kritériem optimality řešení minimalizační dopravní úlohy.
Metoda MODI slouží k rychlému nalezení nepřímých sazeb z ij. Její princip spočívá v tom, že lze najít takové hodnoty duálních proměnných – řádková čísla u i a sloupcová čísla v j , že pro všechny bázické proměnné x ij > 0 (odpovídající obsazeným bazickým polím) platí rovnice: u i + v j = c ij.
Analýza propustnosti
realizované spoje nyní posuzujeme z hlediska množství materiálu, který je po nich přepravován nebo by po nich mohl být přepravován. Propustnost tras představuje maximální objem materiálu, který lze přepravit po dané trase. (Danzitzig)
vysoce propustné – propustné – málo propustné
Analýza perspektivisty
perspektivista tras je chápána jako vliv použití trasy na hodnotu dopravních nákladů. Je to tedy hodnota, podle níž jsou testovány jednotlivé trasy v testu optimality, tj. podle velikosti hodnoty :
r ij = c ij – z ij. pro trasy optimální a alternativní platí r ij = 0…..pro trasy neoptimální je r ij > 0. (jedná se o ty hodnoty, které jsem vypočítala u testu optimality, nejlepší jsou ty nejblíže nulo, protože mi hodnotu kritéria zhorší nejméně…tj. zvednou nejméně).
vysoce perspektivní trasy – perspektivní trasy – neperspektivní trasy
dodatek k metodě váženého součtu : postup řešení
1) převedeme vše na minimalizační nebo maximalizační kritérium podle vztahu y ij = max (y ij ) – y ij. Dostaneme tak pro každou variantu ohodnocení, o kolik je podle příslušného kritéria lepší než nejhorší varianta
2) určíme ideální variantu s ohodnocením h a bazální variantu s ohodnocením d
3) vytvoříme standardizovanou kriteriální matici R, jejíž prvky jsou podle vzorce
y ij – d j
r ij = -----------------
h j – d j
4) pro jednotlivé varianty vypočteme fci užitku:
u = suma v j r ij
5) varianty setřídíme sestupně podle hodnoty fce užitku (nejvyšší dostane 1)
3) Systémová analýza, operační výzkum, modely a modelování
Model: model je záměrně zjednodušený obraz skutečnosti vytvořený pomocí zvolených zobrazovacích prostředků.
a) Operační analýza
Cílem operačního výzkumu je poskytnout exaktní systémové informace pro řešení problémů ve složitých systémech.
Optimalizační modely
- slouží k nalezení nejlepšího řešení problémů,
- možná řešení jsou prvky nějaké konečné či nekonečné množiny
- např. lineární, nelineární, dynamické, stochastické programování nebo vícekriteriální rozhodování
Distribuční a dopravní modely
- slouží k řešení problémů spojených s dopravou či distribucí
Modely plánování a řízení projektů
- modely umožňující časovou, nákladovou a zdrojovou analýzu projektů, ve kterých probíhá více operací, které jsou na sobě závislé
- cílem je zajistit nejvýhodnější průběh těchto operací
Modele teorie rozvrhování
- cílem je najít nejvýhodnější časové a prostorové uspořádání průmyslových operací z mnoha různých hledisek
Modely strukturální analýzy
- bilancují vztahy mezi jednotlivými hospodářskými odvětvími vyhledávají rovnovážný stav systému
- modely Leontijevovy
Simulační modely
- speciální typ modelů, které popisují a napodobují strukturu a chování zkoumaných objektů
- např. hromadné obsluhy, zásob, obnovy a marketingové modely
Stochastické modely
- poskytují informace o systémech s náhodným chováním
Teorie rozhodování a teorie her
- zabývá se popisem a řešení konfliktních situací, kdy důsledky rozhodnutí jsou závislé nejen na rozhodnutí samotném, ale i na dalších faktorech.
4) Teorie rozhodování
- Rozhodovací proces je charakterizován jako proces volby nejvýhodnějšího rozhodnutí z několika možných alternativ rozhodnutí.
- Riziko spojené s výběrem určité alternativy rozhodnutí chápáno jako možnost nežádoucích výsledků, ke kterým by vedla realizace zvolené alternativ za nepříznivých situací.
- Nejistotu můžeme chápat jako nemožnost spolehlivého stanovení budoucích hodnot faktorů ovlivňujících dopady a účinky volby variant.
Vlastnosti rozhodovacího modelu
Rozhodovací situace je charakterizována jako proces volby z alespoň dvou možných variant – alternativ rozhodnutí.
Volba rozhodnutí závisí na možných alternativách rozhodnutí a jejich vlastnostech, na faktorech, které ovlivňují výsledky rozhodnutí, a na vlastnostech těchto faktorů a především na cíli a kritériu rozhodování.
Alternativy a stavy okolností
Možná rozhodnutí pro řešení problému se nazývají alternativami. Alternativy se navzájem musí vylučovat.
Stavy okolností jsou situace, které ovlivňují výsledky jednotlivých alternativ. Stejně jako alternativy se musí vzájemně vylučovat.
Výplatní tabulka
Každá alternativa za odpovídajícího stavu okolností je ohodnocena výsledkem, kterým je určitý hospodářský efekt. Tento efekt se nazývá výplatou.
Výplatní nebo rozhodovací tabulkou se nazývá matice rozměru m x n (jestliže je m alternativ a n stavů okolností), jejímiž prvky jsou jednotlivé výplaty.
Rozhodovací tabulky jsou maticovou formou rozhodovacího modelu. Rozhodovací modely mohou mít též grafickou formu – rozhodovací strom. O nich ale bude pojednáno dále v souvislosti s pravděpodobnostními stromy.
Rozhodovací kritérium
Při volbě se řídíme záměrem a přístupem rozhodovatele k problému.
Jistota a riziko
Důležitým rysem rozhodovací situace pravděpodobnosti pj je realizace jednotlivých stavů okolností. Vektor těchto pravděpodobností p je často nazýván vektorem rizika.
Pokud je rozhodovateli známo, jaký stav okolností nastane, rozhoduje za podmínek jistoty.
Jestliže musí rozhodovat za podmínek úplné nejistoty, rozhodovatel nemá vůbec žádnou představu o tom, jaký bude aktuální stav okolností.
Situace ležící mezi těmito dvěma krajními možnostmi, kdy rozhodovatel sice neví s jistotou, jaký bude aktuální stav okolností, ale na základě různých poznatků a zpráv soudí, který stav okolností to pravděpodobně bude. Může se ovšem mýlit. Pak rozhoduje za podmínek rizika. Riziko je tím větší, čím menší je pravděpodobnost realizace určitého stavu okolností a naopak.
Pro hodnoty p. ve vektoru rizika platí:
4) rozhodování s jistotou: pravděpodobnost pj známého stavu okolností J je rovna 1 a pravděpodobnosti pj ostatních stavů okolností jsou rovny 0
5) rozhodování s rizikem: pro pravděpodobnosti pj realizace stavů okolností platí 0<pj<1 a suma pj = 1
6) rozhodování za nejistoty: pravděpodobnosti pj realizace stavů okolností jsou neznámé
Objektivní a subjektivní pravděpodobnosti
Objektivní p. jsou určovány na základě minulých statistických údajů, jsou stanoveny vždy číselně
Subjektivní p. vyjadřuje míru toho, že jen nastane, na základě osobního přesvědčení rozhodovatele, jsou buď číselné nebo slovní
Možnosti řešení rozhodovacích modelů
Cílem těchto modelů je určení takové alternativy rozhodnutí v závislosti na jednotlivých výplatách, která poskytne rozhodovateli nejlepší výsledek.
Tři základní skupiny metod pro analýzu a řešení:
- volba dominantní alternativy
- volba nejvýhodnější alternativy
- volba alternativy rozhodnutí podle nejvyššího užitku
Dominance alternativ
Dominance neboli převaha jedné alternativy nad druhou je vztahem mezi dvěma alternativami, které definuje jednu z alternativ jako lepší a druhou alternativu jako horší.
Nejsilnější formou dominance je dominance podle výplat, slabší je dominance podle stavů okolností a nejslabší je dominance podle pravděpodobnosti. Dominance podle výplat implikuje dominanci podle stavů okolností a ta implikuje dominanci podle pravděpodobností.
Dominance podle výplat
Je založena na požadavku, aby dominující alternativa poskytovala všechny výplaty lepší nebo stejně dobré jako alternativa dominovaná, aby nejhorší výplata dominující alternativy byla lepší nebo stejná jako nejlepší výplata alternativy dominované. Ve vícekriteriálních variantách tato volba není možná.
Dominance podle stavu okolností
Je založena na požadavku, aby dominující alternativa poskytovala pro každý stav okolností výplaty lepší nebo stejné jako alternativa dominovaná.
Dominance podle pravděpodobností
Pravděpodobnosti hodnot výplat stejných nebo lepších než nějaká hodnota x jsou u dominující alternativy větší nebo stejné jako u alternativy dominované.
Tato forma dominance je založena na kumulativní pravděpodobnosti hodnot výplat. Kumulativní pravděpodobnosti P (v ij >= x) lze vypočítat pro hodnoty výplat v ij a danou hodnotu x podle vztahu
Graf kumulativní pravděpodobnosti P (v ij >= x) je nazýván profil rizika. Poskytuje globální pohled na velikost výplat a odpovídá na otázky
- s jakou pravděpodobností dosáhnout jednotlivé alternativy určité hodnoty výplat? (lze vypočítat dosazením aspirační úrovně)
- jakou minimální výplatu je možné očekávat u jednotlivých alternativ s danou pravděpodobností.
Nejvýhodnější alternativa
Nejvýhodnější alternativa je chápána jako alternativa slibující nejlepší výplatu.
Nejvýhodnější alternativa při rozhodování za jistoty
Kdyby rozhodovatel získal spolehlivou informaci o tom, který stav okolností bude aktuální v bodě realizace jeho rozhodnutí a pokud by tedy takovou informaci rozhodovatel znal, rozhodoval by za podmínek jistoty = zvolil by tu alternativu, která má pro daný stav okolností nejlepší výplatu.
Pokud tedy při rozhodování známe stav okolností sj a jedná-li se o maximalizační kritérium, nejvýhodnější alternativa je vybrána podle vztahu:
Nejvýhodnější alternativa při rozhodování za úplné nejistoty
Pro výběr rozhodnutí řada postupů, při nichž jsou hodnoceny buď výplaty nebo ztráty jednotlivých alternativ a které se liší mírou rozhodovatelova optimismu či pesimismu.
f) maximaxový přístup
- použijeme ho v případě, že „odvážnému štěstí přeje“ a rozhodovatel je tedy ochoten riskovat
- řešením je alternativa, která přinese nejlepší výplatu
- za účelem nalezení maximální výplaty vyhledává rozhodovatel maximální výplatu pro každou alternativu a z nich vybere opět maximum.
g) maximinový přístup (Waldovo kritérium)
- „lepší něco než nic“
- rozhodovatel vybírá mezi nevýhodnými výplatami, aby si z nich vybral tu nejméně špatnou
- podle tohoto kritéria je tedy situace posuzována z hlediska nejhorších možných výsledků
- rozhodovatel nejprve vyhledává minimální výplatu pro každou alternativu a z nich vybere výplatu maximální
h) princip minimaxové ztráty (Savageovo kritérium)
Předchozí mají nevýhodu, že se fixují na jednu určitou výplatu a nepřihlížejí k výplatám ostatním. Je rozumné posuzovat alternativy podle toho, kolik je možno při jednotlivých stavech okolností ztratit vzhledem k nejlepší výplatě, je-li vybrána jiná než alternativa s nejlepší výplatou. Jedná se o použití Waldova kritéria pro matici ztrát.
Při uplatňování minimaxové ztráty se v každém sloupci matice vyhledají maximální výplaty při maximalizačním rozhodovacím kritériu a od těch se odečtou ostatní výplaty ve sloupci.
Pro jednotlivé alternativy se pak určí maximální ztráty. Jako optimum se pak vybírá alternativa a1, která odpovídá minimální z maximálních ztrát. Pro maximalizační kritérium platí
i) princip nedostatečné evidence (Bernoulli-Laplaceův princip)
Tento přístup se snaží zohlednit všechny výplaty a jednotlivé stavy okolností považuje za stejně pravděpodobné tj. rozhodování za podmínek nejistoty je převedeno na rozhodování za podmínek rizika s pravděpodobnostním vektorem s hodnotami
Ohodnocení jednotlivých alternativ je dáno váženým součtem výplat, který je v tomto případě ekvivalentní jejich průměru. Jako nejvýhodnější alternativa se vybírá ta, která vede k nejlepšímu průměrnému výsledku. Tento princip leze použít pro výplatní matici i pro matici ztrát. Při maximalizačním typu výplat i kritéria bude podle výplat vybrána alternativa a1, pro kterou platí
j) Hurwiczovo kritérium
Je založeno na očekávání nejlepších a nejhorších výsledků každé z alternativ. Nejprve je třeba stanovit tzv. optimisticko pesimistický index t pro který platí 0<= t <= 1.
Tento index vyjadřuje očekávaný podíl nejlepší a nejhorší výplaty každé varianty. Hodnota t je mírou optimismu rozhodovatele a hodnota 1 – t je mírou jeho pesimismu.
Dále se vypočítá optimismem a pesimisme vážený průměr nejlepších a nejhorších výplat pro každou strategii.
Nejvýhodnější alternativa při rozhodování za rizika
Předpokládá znalost vektoru rizika (informace o pravděpodobnostech realizace jednotlivých stavů okolností). Vektor označíme p = (p1, p2, p3………. pn)T pro jeho složky platí:
d) očekávaná hodnota výplaty
- používáme Bayerův princip: používáme pro volbu optimální varianty tzv. očekávané hodnoty a pomocí nich se odhadují důsledky rozhodnutí (volíme alternativu s nejlepší očekávanou - střední výplatou, resp. nejnižší očekávanou – střední ztrátou bez ohledu na jednotlivé výplaty).
- očekávaná hodnota výplaty (EMV) představuje vážený aritmetický průměr výplat odpovídajících každé alternativě, kde vahami jsou pravděpodobnosti každého stavu okolností
- pokud se jedná o maximalizaci, bude vybrána alternativa s maximální EMV, tedy
e) očekávaná možná ztráta
Očekávaná možná ztráta (EOL) představuje vážený aritmetický průměr ztrát odpovídajících každé alternativě, kde vahami jsou pravděpodobnosti každého stavu okolností. Podle tohoto pravidla bude vybrána alternativa s minimální EOL, tedy
Princip očekávané možné ztráty vede ke stejnému výsledku jako princip očekávané výplaty.
f) pravděpodobnost dosažení aspirační úrovně
Jinou možností je porovnávání pravděpodobností, s nimiž jednotlivé alternativy budou poskytovat alespoň určitou hodnotu výplaty. Nejvýhodnější alternativa je v tomto případě vybírána podle pravděpodobnosti toho, že její výplata bude lepší než požadovaná úroveň výplat α.
Dodatečné informace
Rozhodování probíhá zřídka za podmínek jistoty i za podmínek úplné nejistoty. Skoro vždy se jedná o rozhodování za rizika. Podstata obtížnosti problému spočívá v tom, že za situace rizika rozhodovatel neví, jaký stav okolností nastane. Disponuje pouze odhady pravděpodobností jejich realizace. Proto si snaží opatřit dodatečné informace, které by potvrdily jeho odhady, případně doplnily jeho informace tak, aby se riziko snížilo, resp. rozhodnutí za rizika se přiblížilo rozhodnutí za jistoty.
Získání těchto informaci: výběrové šetření, předpovědní techniky (jsou však spojeny s dodatečnými náklady).
c) očekávaná hodnota spolehlivé informace (EVPI)
Každá dodatečná informace je spojena s dodatečnými náklady. Proto bude rozhodovatel uvažovat o tom, zda se dodatečné náklady vyplatí. Posouzení jejich účelnosti se provádí porovnáním očekávané hodnoty výplaty,jak je definována pro rozhodování za rizika s očekávanou hodnotou výplaty, jaká by byla dosažena při rozhodování za jistoty, za jednotlivých stavů okolností.
EVPI je definována jako rozdíl očekávané hodnoty výplaty za podmínek jistoty EPC (je definována jako vážený aritmetický průměr nejlepších výplat pro každý stav okolností, kde vahou jsou pravděpodobnosti jejich realizace tedy) a nejvyšší očekávané hodnoty výplaty za podmínek rizika EMV, tedy
Hodnota EVPI se plně shoduje s nejnižší očekávanou hodnotu možné ztráty EOL.
Alternativy výpočtu EVPI:
- jako rozdíl očekávané výplaty za jistoty EPC a nejvyšší očekávané výplaty za rizika EMV
- jako nejnižší očekávaná hodnota možné ztráty EOL.
EVPI umožňuje rozhodovateli posoudit výhodnost resp. nevýhodnost eventuálního dodatečného výběrového šetření za účelem oslabení rizika.
d) očekávaná hodnota výběrové informace
Efektivnost nákladů na výběrové informace se vyjadřuje rozdílem očekávané hodnoty výplaty při uplatnění dodatečné výběrové informace a očekávané hodnoty výplaty bez jejího uplatnění, např. s použitím původního vektoru rizika. Očekávaná hodnota výplaty bez dodatečné informace pro jednotlivé alternativy je hodnota EMV.
Dodatečná výběrová informace je pak představována zpřesněným vektorem rizika např. na základě výběrových šetření. Očekávaná hodnota výplaty při dodatečné výběrové informace EMVS se vypočítá jako
Očekávaná hodnota výběrové informace EVSI je potom rozdíl EVSI = EMVS – EMV (pokud je tento rozdíl výrazně větší než jsou náklady na pořízení dodatečné výběrové informace, je EVSI výhodná)
Někdy se pro posouzení velikosti EVSI formalizuje také ukazatel Ф, nazývaný efektivnost výběrové informace. Ten vyjadřuje srovnání EVSI k očekávané hodnotě spolehlivé informace, resp. k očekávané hodnotě výplaty za jistoty.
Hodnota tohoto poměru se blíží nule při malé efektivnosti a jedné při vysoké efektivnosti výběrové informace.
Postup řešení:
7) nejprve se ověří spolehlivost prováděných odhadů
8) ve sloupcích tabulky musí být součty pravděpodobností rovny jedné
9) pro ověření vhodnosti nového výzkumu se použije složená pravděpodobnost na základě empirie a odhadu jednotlivých stavů
10) tyto ověřené pravděpodobnosti současně umožňují stanovit revidované pravděpodobnosti pro skutečné úrovně poptávky pro všechny možné případy
11) sestaví se doplněný rozhodovací strom, ve kterém jsou zobrazeny výsledky rozhodnutí pro všechny varianty všech rozhodnutí a možných stavů okolností
Rozhodovací stromy
Rozhodovací model může mít maticovou formu, nebo může mít formu grafickou, formu rozhodovacího stromu. Rozhodovací stromy popisují průběh rozhodovací situace pomocí prostředků teorie grafů, pomocí stromů. Rozhodovací stromy obsahují uzly a hrany zobrazující postup rozhodování.
- ukazují, jaké další důsledky a kombinace okolností mohou nastat, zvolíme-li určitou cestu
- nutí promýšlet každou variantu do všech důsledků
- hledají faktory nejistoty pro jednotlivé varianty
Rozhodovací problém je možno zobrazit pomocí grafu, který nazýváme rozhodovací strom. Uzly rozhodovacího stromu se rozlišují na uzly rozhodovací a situační. Hrany se pak dělí na hrany vystupující z rozhodovacích uzlů, které zobrazují alternativy a ze situačních uzlů, které zobrazují stavy okolností. Výplatami v ij pro příslušnou kombinaci alternativa/stav okolností jsou ohodnoceny listy rozhodovacího stromu.
Kořenem rozhodovacího stromu je rozhodovací uzel R, který odpovídá okamžiku rozhodnutí (je ve čtverečku). Na něj navazují hrany jednotlivých alternativ, představující rozhodnutí. Situační (možnostní) uzel M pak odpovídá okamžiku realizace vybrané alternativy ovlivněné jedním ze stavů okolností (je v kroužku). Listy rozhodovacího stromu představují výsledek rozhodovací situace, jsou ohodnoceny výplatami. (rozhodovací tabulky volí situace izolovaně)
Předností stromu je především dodatečné přidání následných rozhodnutí. Následným rozhodnutím míníme opatření rozhodovatele pro případ, že by se realizoval nepříznivý stav okolností. Tato dodatečná rozhodnutí korigují zvolené alternativy tak, aby se zvýšily výplaty. Je rozumné, aby rozhodovatel byl připraven na možná dodatečná rozhodnutí.
Pravděpodobnostní stromy
Pravděpodobnostní stromy představují grafický nástroj pro výpočet důsledků jednotlivých rizikových rozhodnutí, skládajících se z jednotlivých kroků.
Pravděpodobnostní strom zobrazuje průběh realizace rizikového rozhodnutí. Uzly pravděpodobnostního stromu zobrazují jednotlivé kroky rozhodnutí jejichž výsledek je ovlivňován rizikem. Hrany prav. stromu, vycházející z těchto uzlů, zobrazují možné výsledky těchto rizikových kroků včetně jejich pravděpodobností. Listy pravděpodobnostního stromu představují možná ukončení rozhodnutí a jsou ohodnoceny důsledky jednotlivých rizikových kroků.
Slouží k ohodnocení výsledků jediného postupu, který je ovlivňován několika rizikovými faktory, není ho možné použít k jinému modelu (jako rozhodovací strom).
Výhodou prav. stromu je především jednoduchost zobrazení poměrně složitých alternativ rozhodnutí, která jsou posloupnostmi kroků zatížených rizikem. Tyto pravděpodobnosti se vypočítají jako násobky pravděpodobnostního ohodnocení hran ležících na větvi vedoucí z kořenového uzlu do příslušného listu pravděpodobnostního stromu. Nevýhodou je možnost zobrazit pouze diskrétní rizikové faktory jako např. prodáno či neprodáno. Pokud je rizikový faktor spojitý, jako např. velikost poptávky po zboží, je třeba ho aproximovat několika málo hodnotami, např. velká, střední, malá, žádná.
5) Matematické programování
Obecný optimalizační model
Při použití optimalizačních modelů musí být matematicky formulována omezení.
Rozhodnutí, řešení resp. hodnoty jeho prvků či procesů je popsáno vektorem proměnných
x = (x1, x2 , … xn )T ε R n
jehož každá složka vyjadřuje rozsah jednoho procesu, aktivity či prvku rozhodnutí. Možné řešení je omezeno podmínkami, které určují varianty rozhodnutí. Tyto omezující podmínky jsou vyjádřeny vhodnými funkcemi a rovnicemi nebo nerovnicemi, …
Množinou přípustných řešení nazýváme množinu
každý prvek x množiny M nazýváme přípustným řešením. Vektory x, které nesplňují omezující podmínky se nazývají nepřípustným řešením.
Cíl, podle něhož je vybíráno rozhodnutí, je popsán funkcí, která se nazývá účelová nebo kriteriální funkce. Kritériem rozhodnutí je nejčastěji optimalizace výsledku, tedy nalezení maximální nebo minimální hodnoty funkce f (x). Potom se jedná o maximalizační resp. minimalizační model.
Řešení x opt, které splňuje omezující podmínky a v němž účelová funkce nabývá svého optima, resp. maxima se nazývá optimální řešení.
Řešení suboptimálním x sub, tj. řešením které je z hlediska kritéria velmi dobré, účelová funkce v něm nabývá velmi dobré hodnoty, ale nedosahuje své minimální nebo maximální hodnoty.
Klasifikace optimalizačních modelů
Jednokriteriální o.m. : jediné kritérium
Vícekriteriální o.m. : více kritérií (není vždy možno hledat řešení problému pouze z jednoho hlediska)
Z hlediska typu kritéria:
- minimalizační model: jde o nalezení minimální hodnoty účelové funkce
- maximalizační model: jde o nalezení maximální hodnoty účelová funkce.
- cíle modelu (úlohu) : kdy je kritériem rozhodnutí dosažení předem daného výsledku – cíle
Podle typu použitých funkcí se optimalizační modely dělí na
- lineární optimalizační modely: které ve své formulaci využívají pouze lineární funkce a jsou obecně řešitelné simplexovým algoritmem
- nelineární optimalizační modely: v jejichž matematickém popisu je alespoň jedna nelineární funkce
Nelineární modely dále dělíme na
- konvexní modely
- nekonvexní modely
12) Lineární programování
Cílem modelu lineárního programování jakožto optimalizačního modelu je nalézt řešení splňující omezující podmínky, v němž kriteriální funkce nabývá požadovaného extrému. V případě lineárního modelu jsou omezující podmínky vyjádřeny pomocí lineárních rovnic a nerovnic a kritérium pomocí lineární funkce.
Grafické řešení úlohy LP
Prostor řešení: prostor, ve kterém leží všechny přípustná řešení problému. Zobrazujeme zde jak množinu přípustných řešení tak vhodným způsobem účelovou funkci a její chování.
Množina přípustných řešení úlohy LP vznikne jako průnik poloprostorů tj. konvexní množina. Pokud je omezená jedná se o konvexní polyedr. Pokud je neomezená vznikne polyedrický kužel.
Řešení potom nalezneme na přímce zobrazující účelovou funkce ve směru růstu nebo poklesu její hodnoty, která má s množinou přípustných řešení alespoň jeden společný bod. Takový bod je vždy na hranici množiny přípustných řešení (ve vrcholu nebo hraně). Souřadnice těchto bodů jsou hledané hodnoty proměnných optimálního řešení. Optimální hodnota účelové funkce se získá dosazením optimálních hodnot proměnných.
Řešitelnost:
4) množina přípustných řešení je prázdná: omezující podmínky jsou nekonzistentní a model nemá řešení
5) množina p.ř. je konvexní polyedr: lineární optimalizační model má optimální řešení
a. jediné řešení, pokud poslední průsečík přímky účelové fce s množinou přípustných řešení je vrchol polyedru
b. nekonečně mnoho řešení: pokud je tento průsečík hranou či stěnou polydru
6) množina p.ř. je neomezená, je polyedrický kužel: množina v jednom směru nabývá libovolně velkých nebo malých hodnot
Prostor požadavků: je prostor, ve kterém je možno zobrazit vektory koeficientů jednotlivých proměnných (nazývají se aktivity) a vektor pravých stran omezujících podmínek (nazývá se požadavek). Nalezení množiny je chápáno jako skládání vhodných vektorů, tak aby výsledek této operace byl právě vektor pravých stran.
Simplexový algoritmus
Simplexová metoda je nejznámější univerzální metoda pro řešení úloh lineárního programování. Je to metoda iterační, která využívá Jordanovu eliminační metodu doplněnou o dvě kritéria umožňující nalézt optimální řešení.
Jordanova eliminační metoda
Jordanova metoda tedy vede k úpravě soustavy lineárních rovnic do kanonického tvaru.
Povolené eliminační úpravy soustavy rovnice
3) násobení řídící rovnice převrácenou hodnotou řídícího prvku
4) přičtením vhodného násobku řídící rovnice k upravované rovnici
Bazické, nebazické a parametrické řešení
Je-li soustava lineárních rovnic o n proměnných převedena do kanonického tvaru, pak kanonické proměnné, jejichž koeficienty vytvářejí jednotkovou matici, nazýváme bazické proměnné. Všechny ostatní proměnné nazýváme nebázické proměnné. Každé bazické řešení obsahuje nejvýše m nenulových složek.
Bazickým (základním) řešením soustavy lineárních rovnic nazýváme takový vektor x, jehož nenulové složky odpovídají bazickým vektorům.
Degenerované řešení úlohy LP je takové, kde alespoň jedna z bazických proměnných má nulovou hodnotu. Degenerované řešení tedy obsahuje více jak (n-m) nulových složek. Nedegenerované řešení obsahuje právě (n-m) nulových složek.
Pokud budeme považovat hodnoty nebázických proměnných za parametry, dostaneme parametrické řešení soustavy lineárních rovnic, ve kterém jsou vyjádřeny hodnoty bazických proměnných pomocí parametrů – hodnot nebázických proměnných.
Pokud za nebázické proměnné položíme určité hodnoty, dostaneme konkrétní hodnoty i pro bázické proměnné. Takové řešení je nebázické nebo nezákladní.
Matice transformace
Inverzní matici k dané regulární čtvercové matici B označíme B -1 platí pro ně B x B -1 = B x B -1 = E
Matice transformace B -1 je inverzní maticí k matici báze B.
Kritérium optimality řešení: je založeno na zjišťování, zda lze k danému řešení x p soustavy omezujících podmínek najít řešení jiné, které bude mít lepší hodnotu kritéria – účelové funkce.
Alternativní optimální řešení se nazývá takové optimální řešení, které není jediné.
Kritérium přípustnosti
některou z nebázických proměnných x k se nyní pokusíme zařadit místo některé z bazických proměnných x r, kterou z řešení vyloučíme. Přitom chceme, aby nové řešení v bázi B bylo opět nezáporné a hodnota účelové funkce byla lepší.
Simplexový algoritmus vyžaduje lineární optimalizační model s omezujícími podmínkami v rovnicovém tvaru, kanonickém tvaru a s nezápornými hodnotami pravých stran, vektor b. Z tohoto tvaru soustavy omezujících podmínek se určí výchozí bázické řešení.
Dále se provede test optimality. Pokud jsou hodnoty (z – c) rovny nule, výpočet končí, nalezení řešení je optimální. Pokud je kriteriální hodnota záporná, vybere se proměnná x, která má být do báze zařazena. Potom se přejde k testu přípustnosti. Přechod na nové bázické řešení potom vyžaduje provést jeden krok Jordanovy eliminační metody podle vybraného prvku. Dále opět test optimality nového řešení.
Protože simplexová metoda umožňuje řešit pouze úlohy lineárního programování s omezujícími podmínkami v rovnicovém tvaru, v kanonickém tvaru a s nezápornými hodnotami vektoru pravých stran, je třeba každý model do tohoto tvaru transformovat. Nezápornost pravých stran zajistíme vynásobením -1.
Transformace do rovnicového tvaru je založena na myšlence uměle rozšířit počet proměnných modelu tak, aby nové proměnné vytvořily požadovaný kanonický rovnicový tvar soustavy omezujících podmínek
Omezující podmínka lineárního modelu je nerovnice typu <= (>=). Jedná se o kapacitní podmínku, která může být převedena do kanonického tvaru doplněním nezáporné proměnné, jejímž cílem je vyrovnat rozdíl pravé a levé strany podmínky (nezáporné proměnné vyjadřující překročení požadavku). Nazývá se doplňková proměnná typu rezerva (překročení).
Omezující podmínka lineárního modelu je rovnice, ale není v kanonickém tvaru. Tyto podmínky je nutné rozšířit o pomocné proměnné, které pomáhají vytvořit kanonický tvar.
Koeficienty c j v účelové funkci obecně vyjadřují přínos jednotkové proměnné k hodnotě účelové funkce. Nevyužité výrobní zdroje nebo překročení požadavků hodnotu produkce zvýší, proto se oceňují nulovou cenou.
Vyjádření pomocných proměnných z výpočtu docílíme tím, že koeficienty pomocných proměnných v účelové funkci budou velmi nevýhodné. Nazýváme je prohibitivní sazbou (cenou).
Optimální rozhodnutí závisí také na kvalitativních vlivech, které nelze popsat lineární optimalizační modelem. V důsledku vzájemných vlivů modelovaného systému a jeho okolí nebo v důsledku působení náhodných činitelů. Postoptimalizační analýza umožňuje stanovit rozsah přípustných změn v rámci kterých nedochází ke změně optimálního řešení a jak postupovat při vyhledávání nového optimálního řešení.
Matici transformace nalezneme v těch sloupcích výsledné tabulky, v nichž ve výchozí tabulce byly jednotkové vektory
Duální hodnoty pro strukturní proměnné udávají, o kolik se zhorší hodnota účelové funkce, zařadíme-li jednotku daného procesu do řešení, nebo pro doplňkové proměnné udávají, oč se zhorší hodnota účelové funkce, necháme-li jednotku daného činitele nevyužitou.
Alternativní řešení je z hlediska hodnoty účelové funkce řešením optimálním. Získá se zařazením nebázické proměnné s nulovou duální hodnotu (zj – cj) = 0 do řešení, tj. volbou nezáporné hodnoty této nebázické proměnné.
Suboptimální řešení získáme jestliže alespoň jedné z nebázických proměnných x j přiřadíme nenulovou hodnotu. Duální hodnota této nebázické proměnné (zj – cj ) je bližší nule.
Pokud s zabýváme pouze jednou nebázickou proměnnou xk, řešení zůstane přípustné, jestliže požadovaná hodnota splňuje podmínku x k náleží (0, ). Tento interval nazýváme intervalem přípustných hodnot proměnné x k.
Analýza citlivosti se zabývá určováním takového rozsahu změn výchozích údajů LO úlohy, v rámci kterých nedochází ke změně optimální báze.
8) Vícekriteriání optimalizační modely
Modely vícektriteriálního rozhodování (VR) zobrazují rozhodovací problémy, v nichž se důsledky rozhodnutí posuzují podle více kritérií. Zohlednění vícekritérií při hodnocení vnáší do řešení problémů obtíže. Účelem modelů těchto situacích je buĎ nalezení „nejlepší“ varianty podle všech uvažovaných hledisek, vyloučení neefektivních variant nebo uspořádání množiny variant. Přístupy k VR se liší podle charakteru množiny variant či přípustných řešení. Podle způsobu jejího zadávání lze rozlišit dvě skupiny těchto modelů.
- Modely vícekriteriálního hodnocení variant jsou zadány pomocí konečného seznamu variant a jejich ohodnocení podle jednotlivých kritérií.
- Modely vícekriteriální optimalizace mají množinu variant s nekonečně mnoho prvky vyjádřenou pomocí omezujících podmínek a ohodnocení jednotlivých variant je dáno jednotlivými kriteriálními funkcemi.
Vícekriteriální lineární programování
= úloha vektorové optimalizace
Jedná se o modely, které mají množinu variant vyjádřenou soustavou omezujících podmínek a množinu kritérií vyjádřenou kriteriálními funkcemi. Cílem je nalezení požadovaného extrému těchto kritérií na množině přípustných řešení.
Základním pojmem teorie VP je pojem dominované a nedominované řešení.
Jsou-li x i a x j dvě přípustná řešení, potom říkáme, že řešení x i dominuje řešení x j, jestliže platí
Cx i >= Cx j. Přípustné řešení x i je nedominovaným (efektivním) řešením úlohy, pokud neexistuje žádné jiné přípustné řešení, které by jej dominovalo.
Ideální řešení je hypotetické nebo reální řešení, reprezentované ve všech kritériích současně nejlepšími možnými hodnotami.
Bazální řešení je hypotetické nebo reální řešení, reprezentované nejhorším ohodnocením podle všech kritérií.
Kompromisní řešení je řešení, které má od ideálního řešení nejmenší vzdálenost podle vhodné metriky.
Prvky lineárního vícekriteriálího optimalizačního modelu
4) vektor proměnných x, který popisuje jednotlivé složky hledaného rozhodnutí
5) omezující podmínky, které popisují reálná omezení hledaných rozhodnutí
6) vektor účelových nebo kriteriálních funkcí, který popisuje cíle, kritéria hledaného rozhodnutí
Metody řešení úlohy VO
Uživatel si přeje získat výsledek, který má odpovídat různým požadavkům a zároveň je pro ně j konečným rozhodnutím. (závisí především na preferencích uživatele).
Zadání preferencí:
- zadání cílových hodnot kritérií
- forma uspořádání kritérií od nejdůležitějšího k……
- zadáním vah kritérií ohodnocující důležitost kritéria
Pro řešení vícekriteriální optimalizační úlohy existuje řada různých přístupů (metod) lišících se především povahou informace požadované od řešitele, kvalitou poskytovaného výsledku nebo postupem výpočtu.
6) dílčí optimalizace
7) agregace do jediné globální kriteriální funkce, tím se vícekriteriální úloha převádí na klasickou úlohu s jedinou účelovou funkcí
8) zajištění požadované úrovně kritéria formou jeho převodu na omezující podmíku
9) cílovým programováním – pro každou uvažovanou kriteriální fci se předem zadává požadovaná cílová úroveň, které by měla dosáhnout. Smyslem je vyhledat takové kompromisní řešení, které se k této úrovni co nejvíc blíží,
10) interaktivní iterační metody – založeny jsou na dialogu mezi vyhodnocovatelem a řešitelem.
Dílčí optimalizace řešením VO rozumíme řešení, které splňuje všechny omezující podmínky a optimalizuje jedno z kritérií modelu (řešíme tak p jednokriteriáních optimalizačních modelů). Význam je především analytický neboŤ umožňují hodnotit vliv jednotlivých kritérií na výsledek řešení problému, resp. jejich výsledky slouží jako východiska pro jiné metod yVP. Pro každé toto řešení můžeme určit hodnoty všech kritéríí z kj a tyto údaje zapsat do čtvercové kriteriální matice.
Na diagonále leží ideální řešení (nejlepší možné hodnoty kritéri). Bazální řešení je pak charakterizované nejhoršími hodnotami kritérií v jednotlivých sloupcích tabulky.
Agregace kriteriální funkce znamená sloučit všechny kritéria pomocí vhodného operátoru do kritéria jediného. Použitý operátor by měl zajistit, aby žádné kritérium nebylo jeho prostřednictvím zkresleno a nechtěně zvýrazněno či zeslabeno. Základní formy agregace kritérií jsou součinová či podílová a součtová či rozdílová. Příslušnými operátory jsou součin, kriteriálních funkcí nebo jejich součet atd. Pokud jsou všechna kritéria stejného typu, jedná se o jejich součin nebo součet, podíl (rozdíl) se používá jsou-li různého typu.
Operátorem agregace je konvexní lineární kombinace kritérií. Při této formě agregace předpokládáme, že uvažovaná kritéria mají přidelené váhy v i vyjadřující stupeň důležitosti. Jsou z intervalu <0,1>, Váhové koeficienty lze normovat na základě vztahu suma v k = 1. Potom se mluví o normovaných vahách a příslušná lineární kombinace kritérií je konvexní.
Úprava kriteriálních fcí na omezující podmínky: kteroukoliv omezující podmínku lze formulovat jako kriteriální funkci a naopak. Požadavek maximalizace kritéria tak lze formulovat jako požadavkovou podmínku (dosažení alespoň požadované hodnoty kritéria), požadavek minimalizace kritéria lze chápat jako kapacitní podmínku (nepřekročení určité hodnoty kritéria).
Princip tohoto způsobu řešení vychází z následující úvahy. Mějme úlohu VO se dvěma kritériálními funkcemi f1 a f2, u obou funkcí hledáme maximum…..(viz strana 104)
Řešením původní úlohy rozšířené o nové podmínky získáme hledané kompromisní řešení, nebo zjistíme, že požadavky na hodnoty kritérií nejsou splnitelné. S požadovanými hodnotami kritérií lze v obou uvedených postupech experimentovat.
Cílové programování
Vycházíme z výpočtu kompromisního řešení rozšířeného o minimalizaci odchylek od cílových (žádoucích) hodnot jednotlivých kritérií zadaných uživatelem. Vstupními údaji nejsou ovšem pouze cílové hodnoty kritérií. Uživatel dále musí určit preference dosažení jednotlivých cílových hodnot. Tyto preference mohou být vyjádřeny dvěma základními způsoby:
- splnění cílů resp. odchylky od cílových hodnot, lze ohodnotit pomocí vah, přiřazených jednotlivých kriteriálním funkcím. Čím vyšší je důležitost přiblížení se k danému cíli, tím bude zřejmě vyšší váhový koeficient u záporné či kladné diference. Vážený součet odchylek pak vytváří nové optimalizační kritérium, jehož minimalizací lze získat kompromisní řešení.
- vyjádření preferencí jednotlivých kritérií pomocí jejich pořadí na základě jejich důležitosti. Takový model se pak řeší lexikografickou metodou
Modely cílového programování obsahují speciální druh proměnných. Jsou to umělé odchylkové proměnné, představující odchylky od předem stanovených cílových hodnot v kladném nebo záporném směru. Proměnné překročení vyjadřují odchylky v kladném směru, kladné diference a udávají, o kolik je skutečná hodnota daného kritéria vyšší než hodnota cílová d +. V opačném případě jde o proměnné nedosažení, vyjadřující záporné diference d -.
Interaktivní postupy
Interační postupy jsou založeny právě na dialogu mezi rozhodovatelem a řešitelem, přičemž výměna informací probíhá v řadě iterací. Na počátku postupu řešitel vypočte a sdělí rozhodovateli výchozí přibližné řešení. Rozhodovatel pak předá řešiteli informace, na jejichž základě vypočte řešitel zpřesněné řešení a to opět sdělí rozhodovateli. Celý postup se opakuje tak dlouho, dokud se nedojde k řešení, které je ochoten rozhodovatel přijmout.
Metoda ALOP: je založena na principu prohledávání množiny hodnot kriteriálních fcí, nabízí uživateli směry postupu, které on může, ale nemusí akceptovat
Metoda STEM: metoda je použitelná pro situace, které umožňují kompenzaci hodnot kritérií, tj. dostatečné zlepšení hodnoty jednoho kritéria vyváží zhoršení hodnoty jiného kritéria.
9) Vícekriteriální analýza variant
Na rozdíl od VO či VP je v model vícekriteriálího hodnocení variant množina variant zadána ve formě konečného seznamu variant, které jsou ohodnoceny podle jednotlivých kritérií. Toto hodnocení může mít dvě základní formy – ohodnocení ordinální nebo kardinální.
Účelem modelových výpočtů je buď nalezení „nejlepší“ varianty podle všech uvažovaných hledisek vyloučením neefektivních variant nebo stanovení preferenčního pořadí variant z hlediska celého soubor kritérií, přičemž první varianta v tomto pořadí je varianta kompromisní.
Kritéria rozeznáváme maximalizační (čím vyšší hodnota, tím lepší hodnocení) a minimalizační. Celkové hodnocení variant závisí jednak na důležitosti (preferencích) jednotlivých kritérií (interkriteriální preference), jednak na hodnocení variant – alternativ podle jednotlivých kritérií (intrakriteriální preference).
Typy informací o důležitosti kritérií:
5) žádná informace – preferenční informace neexistují
6) nominální informace – i toto je informace přípustná pouze pro preference kritérií mezi sebou – je vyjádřena pomocí aspiračních úrovní tj. nejhorších možných hodnot, při nichž může být varianta akceptována a rozděluje varianty na akceptovatelné a neakceptovatelné
7) ordinální informace – vyjadřuje uspořádání kritérií podle důležitosti nebo uspořádání variant podle toho, jak jsou hodnoceny kritériem
8) kardinální informace – má kvantitativní charakter, v případě preference kritérií se jedná o váhy, v případě ohodnocení variant podle kritéria o konkrétní číselné vyjádření tohoto ohodnocení.
Dominovaná varianta: předpokládejme všechna kritéria maximalizační. Varianta ai dominuje variantu a j, jestliže platí (y i1, y i2..) >= (y j1, y j2….) a existuje alespoň jedno kritérium f l, že y il > y jl.
Paretovská varianta: varianta, která není dominována žádnou jinou variantou, je nedominovaná varianta, často se též nazývá efektivní nebo paretovská. Množina všech nedominovaných variant označíme A N. Množina řešení, o které nelze rozhodnout, které z nich je horší, ale víme, že nelze nalézt lepší.
Ideální varianta je hypotetická nebo reálná varianta, která obsahuje ve všech kritériích současně nejlepší možné hodnoty.
Bazální řešení je hypotetická nebo reálná varianta, jejíž ohodnocení je nejhorší podle všech kritérií.
Kompromisní varianta je řešení, které má od ideální varianta nejmenší vzdálenost podle vhodné metriky. (je jediná varianta doporučená jako řešení problému)
Metody řešení modelů vícekriteriální analýzy variant (VAV) se liší podle typů vstupních informací – modelových dat.
Preference kritérií – informace o důležitosti jednotlivých kritérií
alternativy rozhodnutí – možná rozhodnutí
Kvantifikace ordinální informace
Metoda pořadí
je-li známa ordinální informace – pořadí variant. Nejlepší variantu ohodnotíme číslem p (= počet variant), druhou nejlepší číslem p – 1, atd. Pokud bude několik ohodnocení stejných, pak tyto varianty ohodnotíme průměrným pořadím. Takto kvantifikované kritérium je potom maximalizační. Pokud bychom chtěli kritérium minimalizační, bude ohodnocení varianta postupovat od čísla 1 k p. K určení vah – přísutp několika expertů. Každý z nich seřadí kritéria, nejlepšímu přiřadí k (= počet kritéríí). Sečteme všechny body a vydělíme je celkovým počtem bodů od všech expertů. Suma vah = 1.
Bodovací metoda
stanovíme bodovou stupnici. Smí se používat i desetinná čísla a více variantám je možné přiřadit stejnou bodovou hodnotu. Při maximalizačním typu ohodnocení je varianta ohodnocena tím větším počtem bodů, čím lépe je ohodnocena.
Také tato metoda se pro výpočet vah kritérií používá tehdy, hodnotí-li ji více expertů.
Metoda párového porovnávání
Pokud předpokládáme, že uživatel ohodnotí prvek x jako důležitější než y a zároveň prvek y jako méně důležitý než x, stačí provést počet srovnání.
k (k – 1)
N = ------------------
2
k je počet porovnávaných prvků.
Toto porovnávání se většinou provádí pomocí tzv. Fullerova trojúhelníku.
Saatyho metoda (kvantitativního porovnávání)
Tato metoda slouží k určení vah kritérií, hodnotí-li je pouze jeden expert. Jde o metodu kvantitativního párového porovnávání kritérií. Při vytváření párových srovnání se používá 9-ti bodová stupnice. (1 – rovnocenná kritéria, 3 – slabě preferované kritérium i před j, 5 – silně.., 7 – velmi silně, 9 – absolutně preferované kritérium i před j)
Export porovná každou dvojici kritérií a velikosti preferencí i-tého kritéria vzhledem k j-tému kritérium zapíše do Saatyho matice S. Jsou-li i-té a j-té kritérium rovnocenná, je s ij = 1, preferuje-li slabě i-té kritérium před j-tým je s ij = 3……….
Metody řešení modelů
Bodovací metoda a metoda pořadí
Metoda aspiračních úrovní
Tato metoda je použitelná, je-li známa nominální informace o kritériích, tedy nejhorší přípustné hodnoty kritérií, a kardinální ohodnocení variant podle jednotlivých kritérií.
- konjunktivní metody : připustíme pouze varianty, které splňují všechny aspirační úrovně
- disjunktivní metody : připustíme varianty, které splňují alespoň jeden požadavek
Jsou-li požadavky vyjádřené aspiračními úrovněmi příliš vysoké, přísné, bude množina akceptovatelných variant prázdná. V takovém případě je nutno snížit požadavky, uvolnit požadované aspirační úrovně.
Metoda váženého součtu
vyžadují kardinální informace, kriteriání matici Y a vektor vah kritérií v. Obě konstruují celkové hodnocení pro každou variantu, a tak je leze použít jak pro hledání jedné nejvýhodnější varianty, tak pro uspořádání variant od nejlepší po nejhorší.
Vychází z principu maximalizace užitku. Dosáhne-li varianta ai podle kritéria f j určité hodnoty y ij, přináší tak uživateli určitý užitek, který lze vyjádřit pomocí funkční hodnoty dílčí funkce užitku uj (yij). Funkční hodnoty užitku leží v intervalu <0,1> a čím je varianta výhodnější, tím je vyšší hodnota užitku.
10) Distribuční a dopravní úlohy
distribuční modely pomáhají řešit základní otázky přemíšťování či přiřazování lidí, materiálu a informací, které lze vyjádřit slovy odkud, kam, čím a kudy.
Typy distribučních modelů:
distribuční modely jsou speciálním případem lineárních optimalizačních modelů. Odlišují se speciálními typem matice A, ve které se vyskytuje velice málo nenulových často jednotkových koeficientů.
Mezi klasické distribuční modely patří dopravní modely, jejichž cílem je nalézt optimální způsob přepravy materiálu, zboží apod. Důležitý je počet stupňů přepravy tj. počet míst, meziskladů, přes které je přeprava realizována a počet indexů, tj. počet rozlišovaných způsobů přepravy – dopravních prostředků.
Jednostupňová dopravní úloha
Cílem tohoto modelu je najít takový plán přepravy mezi m dodavateli a n spotřebiteli, při kterém budou celkové přepravní náklady minimální a budou vyčerpány kapacity dodavatelů a uspokojeny požadavky spotřebitelů.
dodavatelé a jejich kapacity
spotřebitelé a jejich požadavky
dopravní náklady – ohodnocení každé trasy dodavatel – spotřebitel
Řešitelnost dopravní úlohy
Dvě podmínky řešitelnosti dopravního problému – úplná zastupitelnost přepravovaného produktu a dělitelnost materiálu a vyváženost úlohy (všichni dodavatelé dohromady musí být schopni uspokojit všechny požadavky spotřebitelů a nic nesmí přebývat a nic nesmí chybět tj. součet kapacit dodavatelů se musí rovnat součtu požadavků spotřebitelů).
Jsou-li tyto dvě podmínky splněny, omezující podmínky dopravní úlohy jsou soustavou lineárních rovnic, které splňuje Frobeniovu větu, a proto jsou řešitelné.
Vyváženost dopravní úlohy
úlohy, ve kterých se součet kapacit rovná součtu požadavků, se nazývají vyvážené, a úlohy, ve kterých se součet kapacit nerovná součtu požadavků, se nazývají nevyvážené dopravní úlohy.
Nevyváženost může znamenat buď přebytek kapacit dodavatelů nebo převis požadavků spotřebitelů.
Převis požadavků spotřebitelů znamená, že kapacity dodavatelů jsou menší než požadavky spotřebitelů… rozšíříme o fiktivního dodavatele. Doplňkové proměnné x vyjadřují zásobování spotřebitelů od fiktivního neexistujícího dodavatele, tedy množství, které spotřebitelé nedostanou. Ceny za tuto přepravu jsou nulové. Pokud je nutno některého spotřebitele skutečně plně zásobit, pak bude použita prohibitivní cena.
Přebytečnou kapacitu, která dodavatelům zůstane ve skladu nahradíme fiktivním spotřebitelem. Ceny jsou opět nulové.
Řešení
algoritmus řešení DÚ
4) nalezení výchozího bazického přípustného řešení pomocí tzv. aproximačních metod:
- metody severozápadního rohu
- indexové metody
- Voglovy aproximační metody
5) test optimality ukáže, zda je možno nalézt jiné základní řešení s lepší hodnotou účelové funkce
6) přechod k lepšímu řešení pomocí tzv. Dantzigových uzavřených obvodů představuje změnu báze, jestliže testované řešení nebylo optimální
Výchozí bázické řešení
Nalezení výchozího bazického řešení je tedy založeno pouze na vhodném výběru tras, kterými se bude nějaké množství přepravovat. Je nutné vybírat trasy s nejmenšími náklady. Omezující podmínky dopravního modelu jsou lineárně závislé, jakmile však jednu vynecháme, zbývající jsou již lineárně nezávislé. Počet bazických proměnných v řešení této soustavy je tedy roven m + n – 1.
Metoda severozápadního rohu
4) v dopravní tabulce vybereme neobsazené volné pole, které má nejnižší možné indexy (severozápadní polev tabulce … tj x 11)
5) vybrané proměnné přiřadíme hodnotu maximálního možného převáženého množství zboží, upravíme kapacity a požadavky
6) dodavatele nebo spotřebitele s vyčerpanou kapacitou či požadavkem vyškrtneme
Indexová metoda
postup se liší pouze při výběru první trasy………nejprve obsahuji volné pole, které má nejnižší sazbu
Vogelova aproximační metoda
Poskytuje řešení velmi blízká řešení optimálnímu. Pro obsazení určité trasy od dodavatele je důležitá relativní výhodnost vzhledem k možnému zvýšení dopravních nákladů, pokud nebude možno využít trasu nejlevnější.
Relativní výhodnost každé trasy se zjišťuje pomocí rozdílu mezi nejvýhodnější a druhou nejvýhodnější sazbou tras od dodavatele (v řádku) reps.ke spotřebiteli (ve sloupci). Tyto rozdíly lze interpretovat jako minimální velikost možné jednotkové ztráty, která by vznikla, kdybychom obsadili nikoli nejvýhodnější, ale až druhé nejvýhodnější pole
3) vypočtou se diference mezi nejvýhodnější a druhou nejvýhodnější sazbou (při minimalizaci mezi nejnižší a druhou nejnižší sazbou)
4) určí se maximální diference, ve vybraném řádku nebo sloupci se vybere trasa s nejvýhodnější sazbou (při stejných maximálních diferencích – obsazuje přednostně pole s nejvýhodnější sazbou z hlediska všech sazeb v matici sazeb – sedlové pole, několik sedlových polí – přednostně obsazujeme to pole, pro které je součet řádkových a sloupcových diferencí maximální)
Dantzigovy uzavřené obvody
představují grafické schéma v distribuční tabulce, které naznačuje jak provést úpravy řešení, jak přesunout převážené zboží z jedné trasy na jinou a přitom nebyly porušeny podmínky dopravní úlohy, tj. velikost kapacit a požadavků.
Dantzigovy uzavřené obvody jsou grafickým znázorněním lineární závislosti proměnných, resp. jejich vektorů koeficientů v omezujících podmínkách dopravního modelu.
Dantzigův uzavřený obvod je uzavřená posloupnost – cyklus na sebe navazujících tras, která obsahuje v řešení již použité trasy a právě jednu trasu novou, jejíž každé dvě sousední trasy mají vždy buď stejného dodavatele nebo stejného spotřebitele.
Množství převáženého materiálu trasami ležícími na uzavřeném obvodu označujeme střídavě znaménky + a -. Nová trasa, resp. množství převáženého materiálu touto trasou bude označeno +, protože touto trasou plánujeme novou přepravu a tedy se bude hodnota proměnné zvyšovat. Chceme-li aby nové řešení bylo bazické, musíme tedy touto trasou převážet maximální možné množství zboží, tedy minimální z hodnot x ij (je transport novou trasou) příslušných trasám, které se nacházejí ve vrcholech uzavřeného obvodu označených znaménkem -.
Test optimality
je založen na porovnání sazeb jednotlivých nebázických tras c rs a příslušných nepřímých sazeb z rs, tj. na porovnání hodnoty skutečných dopravních nákladů touto trasou a nákladů ekvivalentní tras, pomocí níž je materiál přepravován………..
Přepravu trasou x rs nazveme přímou přepravou a cena kombinací přeprav, která je ekvivalentní přepravě od dodavatele ke spotřebiteli. … z rs – c rs <= 0 tato podmínky se nazývá kritériem optimality řešení minimalizační dopravní úlohy.
Metoda MODI slouží k rychlému nalezení nepřímých sazeb z ij. Její princip spočívá v tom, že lze najít takové hodnoty duálních proměnných – řádková čísla u i a sloupcová čísla v j , že pro všechny bázické proměnné x ij > 0 (odpovídající obsazeným bazickým polím) platí rovnice: u i + v j = c ij.
Analýza propustnosti
realizované spoje nyní posuzujeme z hlediska množství materiálu, který je po nich přepravován nebo by po nich mohl být přepravován. Propustnost tras představuje maximální objem materiálu, který lze přepravit po dané trase. (Danzitzig)
vysoce propustné – propustné – málo propustné
Analýza perspektivisty
perspektivista tras je chápána jako vliv použití trasy na hodnotu dopravních nákladů. Je to tedy hodnota, podle níž jsou testovány jednotlivé trasy v testu optimality, tj. podle velikosti hodnoty :
r ij = c ij – z ij. pro trasy optimální a alternativní platí r ij = 0…..pro trasy neoptimální je r ij > 0. (jedná se o ty hodnoty, které jsem vypočítala u testu optimality, nejlepší jsou ty nejblíže nulo, protože mi hodnotu kritéria zhorší nejméně…tj. zvednou nejméně).
vysoce perspektivní trasy – perspektivní trasy – neperspektivní trasy
dodatek k metodě váženého součtu : postup řešení
6) převedeme vše na minimalizační nebo maximalizační kritérium podle vztahu y ij = max (y ij ) – y ij. Dostaneme tak pro každou variantu ohodnocení, o kolik je podle příslušného kritéria lepší než nejhorší varianta
7) určíme ideální variantu s ohodnocením h a bazální variantu s ohodnocením d
8) vytvoříme standardizovanou kriteriální matici R, jejíž prvky jsou podle vzorce
y ij – d j
r ij = -----------------
h j – d j
9) pro jednotlivé varianty vypočteme fci užitku:
u = suma v j r ij
10) varianty setřídíme sestupně podle hodnoty fce užitku (nejvyšší dostane 1)